The hyperboloids are more interesting functions. It's actually easier to think of these as functions of three variables. Examine the function
![]()
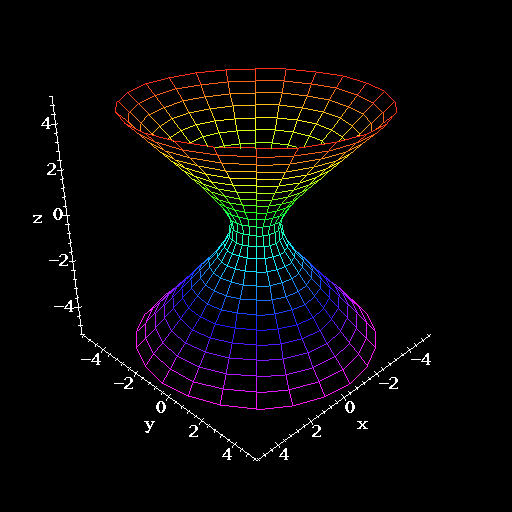
If k is positive, say k = 1 we get a surface that is called a hyperboloid of one sheet. Let's assume that a, b and c are all 1. These constants only scale the surface in the x, y and z directions anyway. What we have now is the function x2 + y2 - z2 = 1 or x2 + y2 = z2 + 1. The contours of this surface are circles. Notice that the smallest of these circles has a radius of 1 (when z = 0.) As z gets farther from zero-in either the positive or negative direction-the circles get larger. The graph of this surface is shown below.
What happens if k = -1? Here, we get the function x2 + y2 = z2 -
1. Clearly, the contours of this are circles, but notice that the circles
cannot exist for |z|<1 since we need ![]() . The circles for
. The circles for ![]() are simply points at the origin. This causes the surface to
actually be made up of two completely separate pieces. It is called a
hyperboloid of two sheets.
are simply points at the origin. This causes the surface to
actually be made up of two completely separate pieces. It is called a
hyperboloid of two sheets.
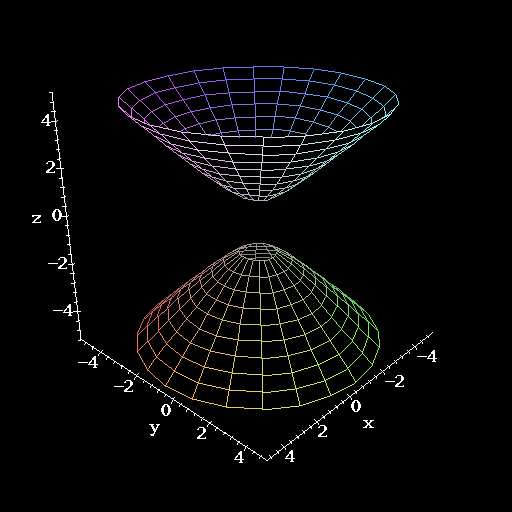
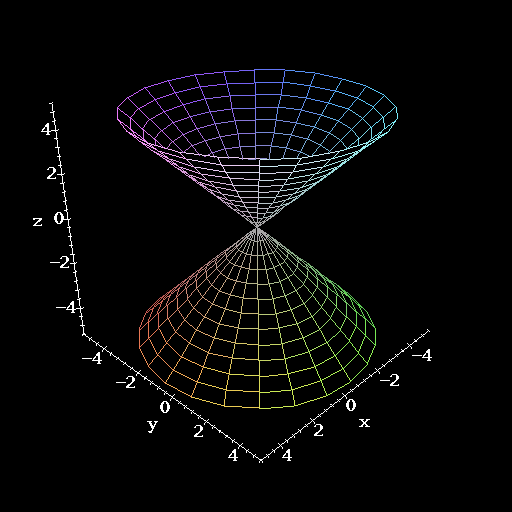
Now at last we come to the dividing case. Let k = 0. We are then trying to graph the surface x2 + y2 = z2. The contours are all circular, with radii from zero on up. The sections of this function are sets of straight lines. When we put this together, we get a cone. Think of the cone as the barrier between the hyperboloid of one sheet and the hyperboloid of two sheets. If you think about it enough, you can envision the three types of surfaces fitting one inside the other, with the hyperboloid of two sheets on the inside, the hyperboloid of one sheet on the outside and the cone fitting neatly between them.
Notice that the function ![]() is the upper portion of
this cone, just as the function
is the upper portion of
this cone, just as the function ![]() is the upper
portion of a one sheeted hyperboloid and so forth.
is the upper
portion of a one sheeted hyperboloid and so forth.