This method relies heavily on the use of the dot product. Let's assume
that we know one point that lies on the plane. Let's call this point P =
(x0, y0, z0). Let's also assume that we know the plane is
perpendicular to the vector ![]() .
.
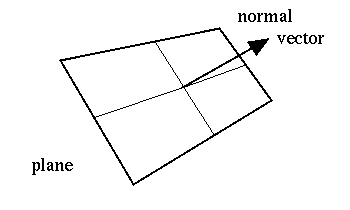
What do we know that we can use to find the equation of the plane? Notice
that if we find a vector that lies in the plane, it must be perpendicular
to ![]() since the plane and the normal vector are perpendicular.
Thus, the dot product of these two vectors is zero. This is an equation,
if only we can find a vector in the plane.
since the plane and the normal vector are perpendicular.
Thus, the dot product of these two vectors is zero. This is an equation,
if only we can find a vector in the plane.
Suppose that the point Q = (x,y,z) also lies on the plane. The
displacement vector from P to Q is then a vector in the plane. The dot
product of this vector, ![]() , and
, and ![]() is zero, so this will be
our equation.
is zero, so this will be
our equation.
![]()
![]()
![]()
As another example, what is the equation of the plane passing through the
point (-1,1,0) with normal vector ![]() ? From
the normal vector, we know immediately that the equation has the form
? From
the normal vector, we know immediately that the equation has the form
x - y + 2z = b.
By plugging in the point, we can compute b as b = (-1) + (1) + 2(0) = 0. Thus the equation for this plane is x - y + 2z = 0.
Note that there are many normal vectors to a plane. Multiplying a vector
by a scalar only changes the length (and possibly orientation if the scalar
is negative) of a vector. Thus, ![]() ,
, ![]() , and
, and ![]() are all normal to the same plane.
are all normal to the same plane.