


Next: Quadratic Functions
Up: Linear Functions-Planes
Previous: Using any three non-collinear
Since we know that the slope of a linear function in the x and y
directions is constant, it is relatively easy to check whether a function
given by a table of values is linear. Suppose the following table
represents a function of x and y.
|
|
X |
|
|
|
| Y |
|
| 3 | 1 |
-1 | -3 |
-5 |
| 4 | 2 |
0 | -2 |
-4 |
| 5 | 3 |
1 | -1 |
-3 |
| 6 | 4 |
2 | 0 |
-2 |
| 7 | 5 |
3 | 1 |
-1 | |
To determine whether or not this represents a linear function, go column by
column to check whether 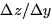 is constant and then go row by
row to check whether
is constant and then go row by
row to check whether 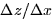 is constant. In this case, any
pair of entries in any column produces
is constant. In this case, any
pair of entries in any column produces 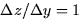 and any pair
of entries in any row produces
and any pair
of entries in any row produces 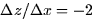 . Thus, this
function is indeed linear.
. Thus, this
function is indeed linear.
However, the function shown in the table below is not a linear function,
since 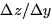 is not the same for any two entries in a column.
is not the same for any two entries in a column.
|
|
X |
|
|
|
| Y |
|
| 5 | 7 |
9 | 11 |
13 |
| 6 | 8 |
10 | 12 |
14 |
| 8 | 10 |
12 | 14 |
16 |
| 9 | 11 |
13 | 15 |
17 |
| 10 | 12 |
14 | 16 |
18 | |



Next: Quadratic Functions
Up: Linear Functions-Planes
Previous: Using any three non-collinear
Vector Calculus
1/8/1998
![]() is constant and then go row by
row to check whether
is constant and then go row by
row to check whether ![]() is constant. In this case, any
pair of entries in any column produces
is constant. In this case, any
pair of entries in any column produces ![]() and any pair
of entries in any row produces
and any pair
of entries in any row produces ![]() . Thus, this
function is indeed linear.
. Thus, this
function is indeed linear.
![]() is not the same for any two entries in a column.
is not the same for any two entries in a column.