The dot product is one of two ways that we can multiply two vectors. The
result of the dot dot product is a scalar quantity. Thus, we start with two
vectors quantities, say ![]() and
and ![]() and form their dot product,
written as
and form their dot product,
written as ![]() . The answer will be a number that, in some
sense, tells us how similar the two vectors are. The more positive the answer
is, the closer the two vectors are in terms of their directions.
. The answer will be a number that, in some
sense, tells us how similar the two vectors are. The more positive the answer
is, the closer the two vectors are in terms of their directions.
One way to calculate the dot product of two vectors is shown below.
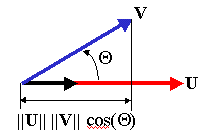
The dot
product is, more or less, the component of the first vector along the
direction of the second vector. Simple trigonometry gives us that this should
be the same as ![]() where
where ![]() is the angle between
the two vectors. In truth, the dot product also includes the length of the
other vector, so that
is the angle between
the two vectors. In truth, the dot product also includes the length of the
other vector, so that
![]()
Now, it is easy to see that if the two vectors have identical directions, then the angle between the vectors is 0, so the dot product will be a maximum. At what angles would the dot product vanish? Watch the animation below to see. In the illustration, both vectors have unit length for simplicity.

Let's use these ideas to come up with a few simple dot products.
![]()
That's not so bad. But what about more general vectors that don't point directly along the basis vectors? Fortunately for us, there are properties of the dot product that help us out.