Just like the integral ![]() gives the area between y=0 and
y=f(x) from x=a to x=b, the integral
gives the area between y=0 and
y=f(x) from x=a to x=b, the integral ![]() gives the total
volume of the solid which lies between z=0 and z=f(x,y) with a cross
section shaped like R.
gives the total
volume of the solid which lies between z=0 and z=f(x,y) with a cross
section shaped like R.
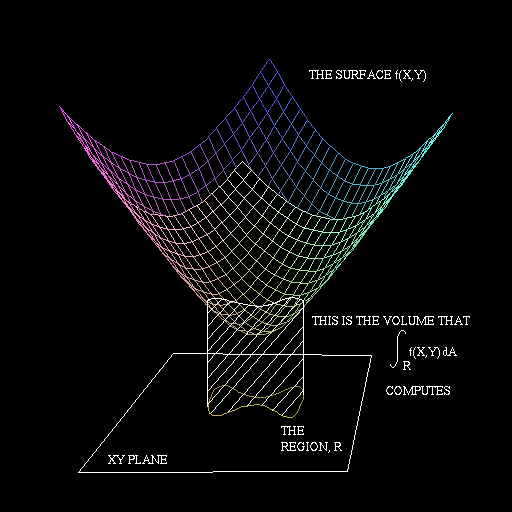

What's the volume of the solid shown here? (The region R is shown more clearly to the right.)
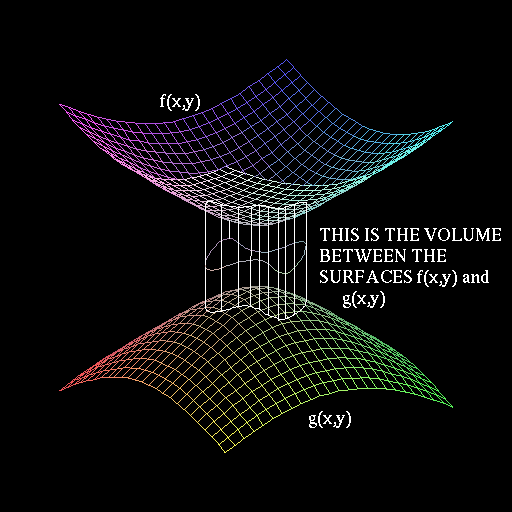
Clearly, ![]() is the volume between z=0 and z = f1(x,y)
while
is the volume between z=0 and z = f1(x,y)
while ![]() is the volume between z=0 and z = f2(x,y).
Thus, the volume between f1 and f2 is the difference of these two
integrals. Since f2 is above f1, the volume of the solid is
is the volume between z=0 and z = f2(x,y).
Thus, the volume between f1 and f2 is the difference of these two
integrals. Since f2 is above f1, the volume of the solid is
![]()
![]()
![]()