- Money in a bank account earns interest at a continuous rate, r. The
amount of money ,
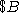 , in the account depends on the amount deposited,
, in the account depends on the amount deposited, 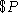 ,
and the number of years, t, it has been in the bank according to the
formula
,
and the number of years, t, it has been in the bank according to the
formula
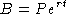 .
.
Find 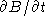 and
and  and interpret each in
financial terms.
and interpret each in
financial terms.
- Let
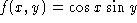 and let S be the surface z = f(x,y).
and let S be the surface z = f(x,y).
- Find a normal vector to the surface S at the point
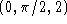 .
. - What is the equation of the tangent plane to the surface S at the
point
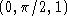 ?
?
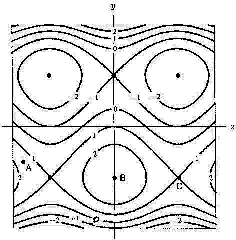
- Consider the points marked A, B, C in the contour plot below. Which of
these appear to be critical points? Classify those that are critical points.
- Let W be the top half of the unit ball,
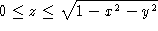 .
Decide whether each of the following integrals is positive, negative or zero.
Give reasons for your decision. [Hint: You can answer this question without
evaluating the integrals.]
.
Decide whether each of the following integrals is positive, negative or zero.
Give reasons for your decision. [Hint: You can answer this question without
evaluating the integrals.]
-
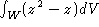
-
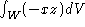
- Show that the equations
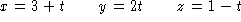
satisfy the equations x + y + 3z = 6 and x - y - z = 2. What does this
tell you about the curve parameterized by these equations?
- For the following vector field, find the line integral along the straight
line segment from the origin to the point (3,3).
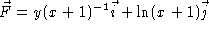
- Calculate the flux of
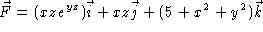
through the disk  in the xy-plane, oriented upward.
in the xy-plane, oriented upward.
- Which of the following vector fields is a gradient field? Find potential
functions for the ones that are gradient fields.
-
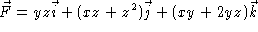
-
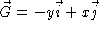
- Consider the vector field
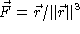 .
.
- Calculate div
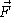 for
for 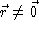 .
. - Find the flux of
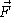 out of a box of side a centered at the
origin with edges parallel to the axes.
out of a box of side a centered at the
origin with edges parallel to the axes.
- Find the circulation of the vector field
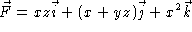 around the circle
around the circle 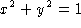 , z = 2, oriented
counterclockwise when viewed from above. [Hint: You can use Stokes's
Theorem.]
, z = 2, oriented
counterclockwise when viewed from above. [Hint: You can use Stokes's
Theorem.]
![]() .
.
![]() and
and ![]() and interpret each in
financial terms.
and interpret each in
financial terms.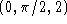 .
.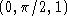 ?
?

![]()
![]()
![]()
![]() in the xy-plane, oriented upward.
in the xy-plane, oriented upward.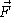 for
for 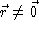 .
.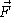 out of a box of side a centered at the
origin with edges parallel to the axes.
out of a box of side a centered at the
origin with edges parallel to the axes.