Section 11.1

#4 and #7. The original table on page 3 of the text book shows the quantity of beef (in pounds of beef per week) that a family with an income of I (in thousands of dollars per year) would buy if the beef had a price of p (in dollars per pound.) Thus, the original table is a numerical representation of the function q = q(I,p). In problem 4, we want to define a new function that gives the total amount of money, M, that a family with an income of I would spend on beef if it had a price of p. This new function should give M in units of dollars per week. Analyzing the units, we see that multiplying q(I,p) by the price p will produce units of (dollars/ pound)*(pounds/ week) = (dollars/ week). Thus, the function M(I,p) can be written as M = q(I,p) * p. A table representation of this is shown below. Likewise, in problem 7, we seek a function which gives the proportion of a family’s income that is spent on beef in a week. A proportion should be dimensionless. If we take the amount of money spent per week (M) and divide by the family’s weekly income (that is, I divided by 52) then we get units of (dollars/ week)/ [(dollars/ year) * (weeks/ year)] = 1. The final function we want is P = P(I,p) = M(I,p)/(I/52) = 52pq(I,p)/I. A table of this information is presented below.

What would these three functions be useful for? The original table of quantities would help a grocer place orders for meat to be sure that he or she would have enough on hand. The second table of money spent, would make pricing decisions and determine profit/ cost ratios. The final information would show how much money a typical family would have left to buy other things (like chicken, rice, etc.)

#11. If we consider the acceleration due to gravity, g, as a function of both the size of the planet, m (its mass,) and the distance we are from the surface, h, then we can determine the dependence of g on both h and m by considering these variables separately.

1. Holding m constant (that is, staying on one planet,) it stands to reason that the further one is from the surface of the planet, the less effect the planet will have on you. This means that g is decreasing as h increases, so that g is a decreasing function of h. If this were not so, then we could never have gotten to the moon, since the pull of the earth would have gotten stronger as we got further away.
2. Holding h constant (that is, staying at the same height above the planet) but letting the planet’s mass change, we would expect a larger planet to have a greater pull on us, so that g is an increasing function of m. This explains why one can jump higher on the moon. It is smaller so that g is also smaller.

#12. We are given a table of values of wind chill (ie. The temperature, T, "it feels like") as a function of the actual temperature, t, (in degrees Fahrenheit) and the wind speed, w, (in mph.) One can view T as a function of the two variables t and w.

1. If the actual temperature is t = 0 and the wind speed is w = 15 then the table shows that T(0,15) = -31, so that it would feel like 31 degrees (F) below zero!
2. If the actual temperature, t = 35 and it feels like T = 22, we see that T(35,10) = 22 so that a wind speed w = 10 would result in these conditions.
3. If t = 25 and T = 20, we note that there is no speed given on the table for w which would give T = 20. However, we note that T(25, 5) = 21 and T(25,10) = 10. T = 20 is between these two, and is closer to 21 so we would assume that a wind speed between 5 and 10, but closer to 5 would give T = 20 at t = 25. Estimating, we could take w = 5.5.
4. Likewise, there is no value of t on the table so that T(t,15) = 0. However, 0 is between T(25,15) = 2 and T(20,15) = -5, so we might guess that t = 3.1 would result in T = 0 at w = 15.

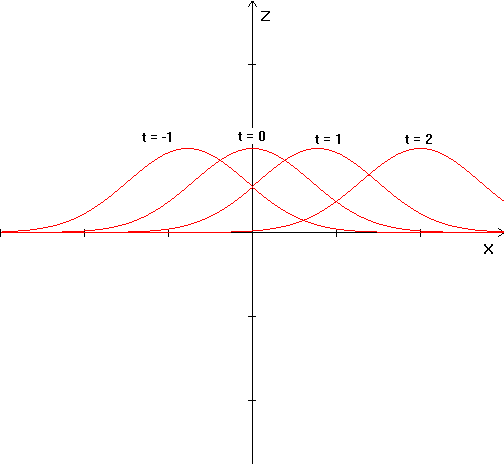
#18. The functions f(x,0) and f(x,1) represent two cross sections of the function f(x,t) with t fixed. Since f(x,t) represents the height above equilibrium that a piece of the vibrating string at position x at time t occupies, we note that fixing t is like taking a photo of the string at that time. It shows the height of each piece of string at that instant of time. Thus, f(x,0) is a picture of the string’s displacement right as the string is released. The function f(x,1) shows the same string at t = 1, when it has relaxed a bit and started to sink towards equilibrium.

Section 11.2

#3. Starting at the point (-1,-3,-3) and facing the yz plane with our head upright (toward +z) would place us looking toward the positive x axis (see diagram.) Walking forward 2 units would bring us to (-1+2,-3,-3) = (1,-3,-3). Turning left would face us toward the positive y axis so that walking forward 2 units brings us to (1,-3+2,-3) = (1,-1,-3). The observer on page 9 would see us in front of the yz plane (positive x coordinate,) left of the xz plane (negative y coordinate,) and below the xy plane (negative z coordinate.)

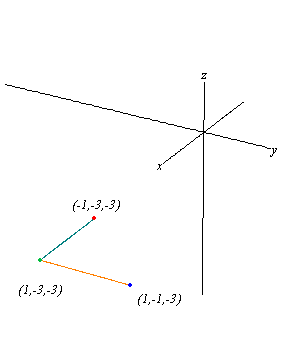
#8. To find a formula for the shortest distance between the point (a,b,c) and the y axis we will need two things: the coordinates of a point on the y axis that is closest to (a,b,c) and the distance formula. In general, a point on the y axis has x = 0 and z = 0, but y can take any value. What value of y puts the point (0,y,0) closest to (a,b,c)? Draw a picture and remember that the shortest distance will create a line that would be perpendicular to the y axis. Thus, the closest point on the y axis is (0,b,0). The distance formula then gives the distance as . An alternative to this method would be to simply write down the distance between (0,y,0) and (a,b,c) as a function of y and then minimize this function over the possible y values. You should get the same end result.

#9. The set of all points whose distance from the x axis is 2 would form a cylinder of radius 2 which is centered so that its axis is the x axis.

#10. The set of all points (x,y,z) whose distance from the x axis (a point on the x axis would have coordinates (x,0,0) ) equals the distance to the yz plane (a point on the yz plane has coordinates (0,y,z) ) would be the set of all points (x,y,z) such that

. This can be simplified to the form which is the equation of a cone centered along the x axis. See the illustrations on page 48 of the text for a picture.

#14. The center of this rectangle is at (1,1,-2). If the length of 13 is parallel to the y axis, then the front and back of the solid are at y = (1+13/2) = 7.5 and y = (1-13/2) = -5.5, respectively. The top and bottom are at z = (-2 + 5/2) = 0.5 and z = (-2 – 5/2) = -4.5, since the height of 5 is parallel to the z axis. Lastly, the sides are at x = (1 + 6/2) = 4 and x = (1-6/2) = -2. These six equations are the equations of the planes which make up the six faces of the object. Each corner is a point that lies on three of these faces. Drawing a simple picture in 3D of the solid will give the corners coordinates (-2,-5.5,0.5), (4,-5.5,0.5), (4,-5.5,-4.5), (-2,-5.5,-4.5), (-2,7.5,0.5), (4,7.5,0.5), (4,7.5,-4.5) and (-2,7.5,-4.5).

#15. Using the distance formula (given on page 12) gives us the following (we denote the distance from point P to point P_I by d(P, i).) We find: d(P,1) = , d(P,2) = , d(P,3) = and d(P,4) = . Thus, point 4 is closest to P.

#16. A line through the origin, lying in the xz plane, and such that as x increases, z decreases, would look much like the diagram to the right. Note the use of the blue lines and the green lines to help indicate perspective. Use this technique in your own drawings in order to help add The Third Dimension.

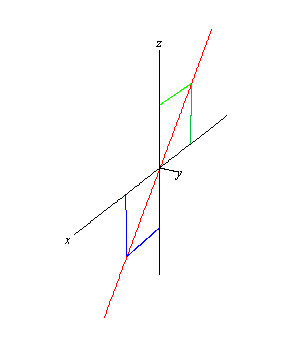
#20. The equation given represents a sphere of radius 2 centered at the point (1,-3,2). Why is this? The definition of a sphere is the set of all points (x,y,z) such that each is the same distance (called the radius) from the center of the sphere. Thus, we can use the distance formula to write down that the distance between the point (x,y,z) and the point (1,-3,2) is 2. Squaring both sides results in the equation shown in problem 20 on page 14.

1. In order to determine whether the sphere intersects the xy coordinate plane, we should plug in the equation of that plane, namely z = 0. If we put this into the formula for the sphere and rearrange, we find that which is the equation of a circle centered at x = 1, y = -3 with a radius 0 lying in the xy plane. Thus, it is really a point (1,-3,0) not a circle. This indicates that the sphere is just tangent to the xy plane (like a ball resting on a table, with the ball touching the table at x = 1, y = -3. Similarly, we find that the sphere crosses the yz plane (x = 0) in the circle which indicates a circle of radius centered at (0,-3,2) lying in the yz plane. This indicates that the sphere actually crosses the plane, rather than being tangent to it. The last coordinate plane, the xz plane (y = 0,) does not touch the sphere, since the resulting equation is for a circle with an imaginary radius.
2. In a similar fashion, we can determine if the sphere touches the x axis (y = z = 0) or the y axis (x = z = 0) or the z axis (x = y = 0.) At most we expect two solutions, although we could get one or zero solutions. For this sphere, however, we find that the coordinate axes completely miss the mark and there are no solution for any of the three situations.

Section 11.3

#3. I encourage you to use WinPlot to graph each of these functions as a surface. This will help you in making a decision.

1. This equation has parabolic cross sections. In fact, this surface is called a paraboloid and looks exactly like a bowl, sitting at (0,0,0) and facing the positive z axis.
2. This equation represents the same surface as (a), except it has been flipped over and shifted up (+1). Thus it represents an upside down bowl, which would not hold water. By the definition of the problem, then, this is not a bowl (and it is certainly not a plate.)
3. This is a linear function (discussed in detail in 11.5) so the surface must be a plane, which is flat, so we define it to be a plate.
4. If you square both sides of this equation, you find that this is the equation for a sphere of radius centered at the origin. The negative in front of the square root in the original equation means that we want the lower (southern) hemisphere of the sphere, rather than the entire surface. Thus, this function represents a bowl.
5. This is also a linear equation. In fact, it is a plane parallel to the xy pane, shifted up 3 units. Thus, it is a plate (which is floating in the air.)

#5. Note that (a) and (b) have circular symmetry (since the contours are circles and the only appearance of the independent variables x and y is of the form ). Thus, only graphs (I) and (V) could match. Since (b) is always negative (e to a power is always positive, but the negative sign in front reverses this) we conclude that (b) must be (V). This leaves (a) to be matched with (I). Equation (c) represents a linear function, whose graph is a plane, so that it must be (IV). Equation (d) is missing any x dependence, indicating that it is a "cylinder" (see page 18-19). It must look the same for any value of x. Only graph (II) matches this (note that its cross-sections for fixed x are all upside down parabolas in a plane parallel to the yz plane.) That leaves (e) to be matched with (III).

#6. This problem deals with a verbal description of a surface. The independent variables are pizza and cola and the dependent variable is happiness. To answer the questions, try looking at the surfaces (I) –(IV) in terms of sections. Fix either the number of pizzas or the amount of cola and compare the graphs.

1. For this situation, more pizza and more cola always increase happiness. Graph (IV) is the only graph which matches this.
2. Here, there comes a point where more pizza decreases happiness. There is also a point where too much cola decreases happiness. Thus, happiness should increase with pizza and cola for a while and then decrease. Graph (I) matches this.
3. Too much cola decreases happiness, but more pizza is always better. This must be graph (III) since graph (II) indicates that too much pizza is bad, but too much cola is good.

#8. In order to answer this question, look at each of the surfaces as a series of sections. Figure 11.37 shows what the sections should look like. At y = 0, the surface should be level at z = 0. For positive y values (like f(x,1) and f(x,2)) we see that the surface should be concave upward, have reflective symmetry in the x direction across the z axis, and should get steeper as y increases. The same is true for the negative y values, except that the surface should be concave downward. Thus, only graph (IV) works, since the others lack the reflective symmetry in the x direction (among other things.) One could also use the fact that f is negative for negative y and positive for positive y to answer this question. To get a better feel for the surface, use WinPlot to graph .

#9. To answer this question, build a quick (and easy) visual aid. Take a sheet of paper and fold it in half along the diagonal from the upper left to the lower right corner. Now fold each half up so that you can place the paper down and have a tent-like structure. Label the lower edge of the paper with t increasing to the right and the left edge with x increasing down the page. The origin should be on the hump in the center. This represents the surface shown in figure 11.39.

1. To answer this, draw the lines t = -1, 0, 1, and 2 on your paper. These lines should all be parallel to the left edge of the paper, but at different distances out. Now imagine turning your paper so that the x axis points right, the z axis up (the hump) and the t axis straight away from you. What would the line t = -1 look like? Draw this. Now, on the same xz axes draw the other lines. You should get something like this:
2. The center of the wave profile is moving to the right as t increases so the wave is moving to the right.
3. To see what this would look like, take your folded paper, rotate it ninety degrees, and label the left edge with x increasing down the page, and t increasing to the right along the bottom edge of the page.