Homework Three

Homework Three

Section 12.2

#8. The velocity vector of a moving object is always tangent to the path of the object. This leads us to draw the velocity at P as an arrow pointing straight up the page, the velocity at Q as a vector pointing left and the velocity at R as a vector pointing mostly down the page. Since the car speeds up along the straight parts and slows down on the curves (a good practice) the arrow at Q should be the longest, and the arrow at P the shortest.

#9. Given that acceleration is the rate of change of velocity, and velocity is a vector, we also know that acceleration is a vector. Even if the car travels at constant speed, if the velocity vector changes direction, then there is an acceleration. Since the track is almost straight at point Q, we know that the acceleration vector points along the motion of the car (ie. Parallel to the path) if there is any acceleration. Since the car is presumably speeding up, the acceleration should be an arrow pointing left at Q. At point P, the path of the car is curving to the right, which means that the acceleration vector at P points to the right. At point R, the acceleration should be a short arrow pointing to the left, since the track gently curves here.

#10. From the picture, we know that if the particle had speed v before impact, then the velocity of the particle before impact can be written in components as (v cos(60), -v sin (60)). The (-) sign is due to the original motion being in the -y direction. After the impact, the particle loses 20% of its speed, so its new speed is (1-0.20) v = 0.8 v. Thus, after impact, the components of the velocity vector are (0.8 v cos(60), 0.8 v sin(60)).

#13. The plane has a heading given in components (two dimensional, with +x to the east and +y to the north) as (700 cos(45), 700 sin(45)) since it is headed northeast (45 degrees north of east) at 700 km/hr. The wind has velocity (-60,0) since it blows due west at 60 km/hr. The resultant motion of the plane is then given by the sum of these two vectors:

(-60 + 700 cos(45), 700 sin(45)) ~ (435, 495). This can also be written as a speed of 659 km/hr at a heading of 48.7 degrees north of east.

#15. For a plane heading due east and climbing at 80 km/hr, we can write the velocity vector as (v_east, 0, 80). Furthermore, if the airspeed of the plane is 480 km/hr, we know that v_east = Sqrt(480*480 - 80*80) ~ 473 km/hr. The wind has a velocity of (100 cos(45), 100 sin(45)) so the ground velocity of the plane is the sum of these vectors:

(100 cos(45) + 473, 100 sin(45) + 0, 0 + 80) ~ (543.7, 70.7, 80). The ground speed is then the magnitude of this vector which is approximately 554.1 km/hr.

Section 12.3

#3. Given A = (0,2,1) and B = (-3,5,4) we find that A * B (the dot product) is (0)(-3) + (2)(5) + (1)(4) = 14.

#9. If two vectors are perpendicular, then their dot product is zero. For the vectors (t, -1, 1) and (t, t, -2) this condition amounts to t^2 - t - 2 = 0. Using the quadratic formula (or simply factoring) we find that t = -1, 2 will satisfy the equation, making the two vectors perpendicular. For the two vectors to be parallel, they must be scalar multiples of each other. This implies that (for some constant a) we have a(t,-1,1) = (t,t,-2) so that we have three simultaneous equations to solve: at = t, -a = t, and a = -2. It should be clear that there is no way the first and third equation can be true at the same time, since the third requires a = -2, and the first requires a = 1. Thus, there are no values of t for which the two vectors are parallel.

#11. Recall that the equation of a plane with a normal vector (n_1, n_2, n_3) and passing through the point (x_0, y_0, z_0) is just n_1 (x-x_0) + n_2(y-y_0) + n_3(z-z_0) = 0, as given by the dot product of the normal vector with a vector from the point (x,y,z) to the point (x_0, y_0, z_0) lying in the plane. Thus, the equation of the plane in this problem is given by (-1) (x - 1) + (2)(y-0) + (1) (z - 2) = 0. Solving for z we find: z = x - 2y + 1.

#17. If two planes are parallel, then their normal vectors are scalar multiples of each other. Choosing the simplest multiple, 1, we take the normal vector for the new plane to be the same as the normal vector for the original plane, given by 3x + y + z = 4. The normal vector is simply the coefficients of the variables x, y, and z when written in this form, so that the normal vector is (3,1,1). Since the plane must pass through the point

(-2,3,2) we know that the equation can be written as 3(x+2) + (y-3) + (z - 2) = 0.

#21. The angle between two planes is simply the angle between the normal vectors of the planes. Thus, we want to find the angle between the vectors A = (5,3,2) and B = (1,3,2). Using the dot product, we see that cos(angle) = (A * B)/ ||A|| ||B|| = (5 + 9 + 4)/ Sqrt(38) Sqrt(14) so that (angle) ~ 38.7 degrees.

#22. Assigning coordinates to the corners of the gym so that the x axis runs along the length, the y axis along the width and the z axis along the height, we can see that the stringers can be represented by vectors going from one corner to the other. One vector is from the point (0,0,0) to the point (200,80,25) so it is A = (200,80,25). The other vector is from the point (0,80,0) to the point (200,0,25) so it is B = (200,-80,25). The dot product of these two vectors is (200)(200) + (80)(-80) + (25)(25) = 34225. The magnitude of each vector is Sqrt(47,025) so the cosine of the angle between the vectors is (34,225)/(47,025) ~ 0.7278.

#25. Using the definition of genetic distance as the angle between the genetic vectors of the two populations, we want to calculate the angle between the English and the Bantu and compare this to the angle between the English and the Koreans. The English vector is given by E = (0.20, 0.06, 0.06, 0.66). The Bantu vector is B = (0.10, 0.08, 0.12, 0.69) and the Korean vector is K = (0.22, 0.00, 0.20, 0.57). The magnitudes of these vectors are ||E|| = Sqrt(0.4828) ~ 0.6948, ||B|| = Sqrt(0.5069) ~ 0.7120, and ||K|| = Sqrt(0.4133) ~ 0.6429. We see that E * B = 0.4874 and E * K = 0.4322. The angle between the English and Bantu is then arccos(0.4874/(0.6948*0.7120)) ~ 9.854 degrees and the angle between the English and Korean is arccos(0.4322/(0.6948*0.6429)) ~ 14.632 degrees. The English and Bantu are then more closely related.

#29. Note that if U * W = V * W then we have (U * W - V * W) = 0. Using the properties of the dot product (namely, the distributive property in reverse,) we see that this implies (U - V) * W = 0. This can only happen in three cases:

(a) The vector (U - V) is perpendicular to the vector W. This can't happen since this requires a particular choice of the vector W.

(b) The vector W is the zero vector. This can't happen for the same reason that (a) doesn't work.

Section 12.3

#6. (2,-3,1) X (1,2,-1) = [(-3)(-1) - (1)(2)]i - [(2)(-1) - (1)(1)]j + [(2)(2) - (-3)(1)]k = i + 3j +7k.

#7. A X B = [(1)(2) - (-1)(-4)]i - [(3)(2) - (-1)(1)]j + [(3)(-4) - (1)(1)]k = (-2,-7,-13). To verify that this is perpendicular to both A and B, we use the dot product:

(a) A * (-2,-7,-13) = (3)(-2) + (1)(-7) + (-1)(-13) = 0.

(b) B * (-2,-7,-13) = (1)(-2) + (-4)(-7) + (2)(-13) = 0.

#8. In order to compute tan(angle) from the given information, use the geometric ideas of the cross product and dot product. We know the cross product is (2,-3,5) and the dot product is 3. The magnitude of the cross product is then Sqrt(38). Note that

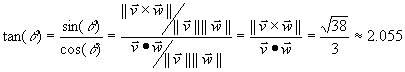#12. Given these points we follow three steps:

(a) Find two displacement vectors in the plane: A = (-2-3, 1-4, 0-2) = (-5, -3, -2) and B = (3-0, 4-2, 2-1) = (3, 2, 1) are two possible choices.

(b) Find a normal vector to the plane by forming the vector A X B = (-1,1,1).

(c) Take the dot product of the normal vector from (b) and a displacement vector from one of the three given points (say (0, 2, 1)) to the point (x, y, z) which is assumed to be in the plane. Since these vectors are perpendicular, the result must be zero, so we have the equation of the plane as: (-1) (x - 0) + (1) (y - 2) + (1) (z - 1) = 0, which can be rewritten as z = x - y + 3.