- (a)
- At the point (-1,2) on the graph of f(x,y) the discriminant, D =
3, fxx = 2 and grad
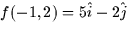 . The point
(-1,2) is
. The point
(-1,2) is
a. a local maximum b. a local minimum c. a saddle point d. none of these - (b)
- A student answers that the directional derivative of f(x,y) in the
direction of
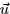 is
is 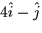 . This answer is incorrect
because:
. This answer is incorrect
because:
a. 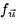 should be a scalar
should be a scalarb. 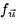 should be a unit
vector
should be a unit
vectorc. neither (a) nor (b) is the correct reason d. there is not enough information - (c)
- Suppose that f(1,-1) = 5, fx (1,-1) = 2, fy(1,-1) = -1. The
equation of the plane that is tangent to f at (1,-1) is
a. z = -(x-1) + 2(y+1) + 5 b. z = 2(x+1) - (y+1) + 5 c. z = 2(x-1) - (y+1) + 5 d. z = -(x+1) + 2(y-1) + 5 - (d)
- The maximum rate of change of z = f(x,y) at the point (a,b) is
a. grad f(a,b) b. 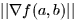
c. | fx(a,b) + fy(a,b)| d. 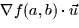
- (a)
- Consider the function z = f(x,y). Construct a new function g(x,y,z) so that the level surface g = 0 corresponds to the surface z = f(x,y).
- (b)
- Relate the gradient of g to the gradient of f using the function g constructed in the previous part.
- (c)
- Using local linearity, explain the relationship between grad g and the surface z = f(x,y). Note that this is a geometric version of the previous part.
- (a)
- Find all first and second partial derivatives of f.
- (b)
- Find the gradient of f.
- (c)
- Find the directional derivative of f at the point
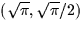 in the direction of the vector
in the direction of the vector 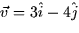 .
.
R(S,V) = 19 S(1/12) V(1/2).
Fox would like us to decide the optimum number of each type of scence to include in a show. However, each sexual scene costs $1000 to produce and each violent scene costs $3000. If the total budget of the show is $28,000, answer the following using complete sentences.- (a)
- Set up and explain the system of equations needed to solve the constrained optimization problem described above.
- (b)
- Solve the system in the previous part.
- (c)
- Find and interpret the Lagrange multiplier for this problem.