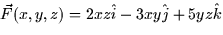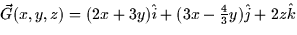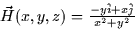Return to Other Sample Exams.
FOURTH HOUR MAKEUP EXAM
MATH 223
Instructor: Kris Green
May 5, 1998
10:00 - 10:50 am
- 1.
- Consider the motion of a particle described by the parametric curve
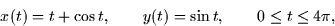
- (a)
- What is the particle's velocity?
- (b)
- At t = 0, the particle flies off along the tangent vector at
constant velocity. Parameterize the resulting motion.
- (c)
- Another particle is traveling in a circle of radius 3, centered at
(2,2) traversed counter-clockwise so that at t = 0 it is at (5,2).
Give an implicit (ie. f(x,y)=0) form of this motion.
- (d)
- Will the motion of the first particle ever satisfy the relation
that you found in (c)? If so, when?
- (e)
- What does your answer to (d) tell you about the motion of the two
particles?
- 2.
-
- (a)
- Let x(t) and y(t) be given as shown below. Sketch a graph
(including the starting point and direction of motion) for the motion in
the xy plane.
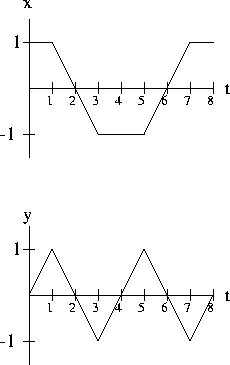
- (b)
- Using Green's Theorem, compute
![$\int_C [(2xy - 5y)\hat{i} + (x^2 -
y^2)\hat{j}]\cdot d\vec{r}$](img3.gif) where C is the path in part (a). Note that
you must modify Green's Theorem (slightly) to use it in this case.
where C is the path in part (a). Note that
you must modify Green's Theorem (slightly) to use it in this case.
- 3.
- Given that
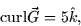
compute 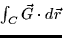 where C is the triangle in the
plane z = (17/10) - (3/5)x - (1/10)y with vertices at (1,1,1),
(-1,3,2), and (-2,-1,3) traversed in this order. (Hint: Use Stokes'
Theorem.)
where C is the triangle in the
plane z = (17/10) - (3/5)x - (1/10)y with vertices at (1,1,1),
(-1,3,2), and (-2,-1,3) traversed in this order. (Hint: Use Stokes'
Theorem.)
- 4.
- Which of the following vector fields are conservative? For those
that are conservative, compute the scalar potential function. For those
that are not, explain why they are not.
- (a)
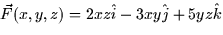
- (b)
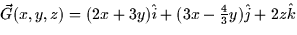
- (c)
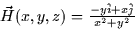
- 5.
- For the illustrated paths and vector fields below, decide whether the
line integral
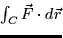 is positive, negative, or
zero.
is positive, negative, or
zero.
- (a)

- (b)
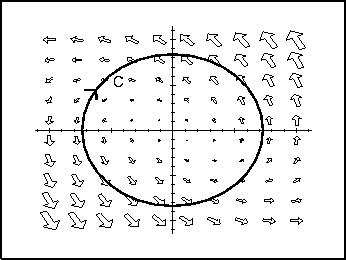
- (c)
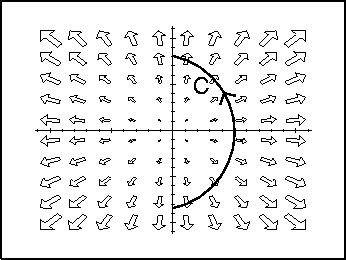
- (d)
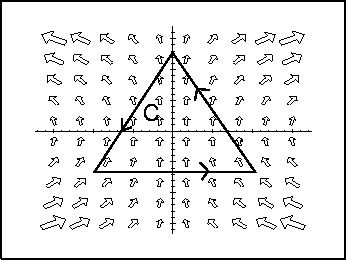
Vector Calculus
8/20/1998
![]()

![$\int_C [(2xy - 5y)\hat{i} + (x^2 -
y^2)\hat{j}]\cdot d\vec{r}$](img3.gif) where C is the path in part (a). Note that
you must modify Green's Theorem (slightly) to use it in this case.
where C is the path in part (a). Note that
you must modify Green's Theorem (slightly) to use it in this case.
![]()