(Return to GMST 570 Resources)
Formally, a function is any object that takes an input (or set of inputs) and produces a single output (or set of outputs). Functions can be thought of as machines: the input goes in, the "function machine" does something to it, and an output comes out. It is important that each input (or set of inputs) only produce a single output (or set of outputs). Otherwise, the machine doesn't know which output to give.
For example, a blender can be considered a function for producing milkshakes: milk and ice cream go in (the input), the blender does something (whirls it around real fast), and a tasty, frothy milkshake results (the output). Here's where the idea of "one input produces one output" is important: imagine how weird it would be if sometimes, you put the milk and ice cream into the blender and you got something that wasn't a milkshake (say, a turkey sandwich). That wouldn't make much sense at all.
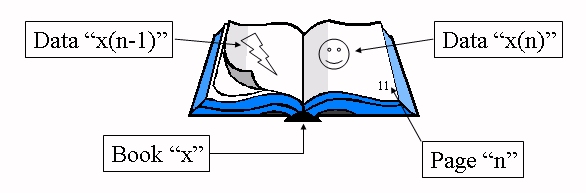
Many of the functions you have encountered are continuous functions: their inputs are real numbers and their outputs are real numbers. For example, f(x) = 2x + 1 is a function that takes any real number, x, and returns the value of 2x + 1. So, f(3) = 2(3) + 1 = 7; f(1.4) = 3.8; and so on. In this course, we have started by studying discrete functions. These are functions that have integer inputs, but may return any real number (possibly). The way I think of discrete function is illustrated below.
Discrete functions as a book:

The picture shows that x(11) = "a smiley face" and x(11-1) = x(10) = "a lightning bolt".
If you want to use this idea for a continuous function, you need to imagine a book with so many pages that they cannot be counted or put in any particular order (between any two pages, there is another page!). Instead of an integer "n" to reference the pages, you have to use an infinitely precise rule to measure how far from the beginning of the book you want to go.