There are many different ways to represent a function of two variables
graphically. We'll discuss a fairly common method here and save the others
for later in this chapter. The method we'll concentrate on now is called a
contour map. Suppose you want to the high temperature for the day
in Topeka, Kansas from a weather map. Most newspapers and weather shows
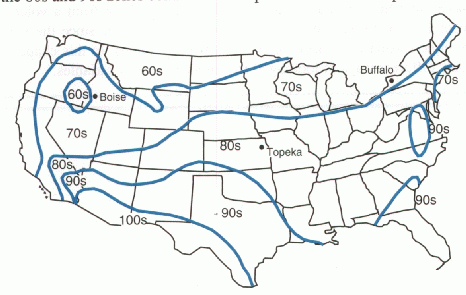
use a map that looks something like this.

This is one example of a contour map. The independent variables (the ones we select) are the latitude and longitude. The dependent variable is the high temperature for that latitude and longitude. The dark lines, or contours connect all the points that share the same value of the temperature. Thus, all the points along the T = 80 line are at eighty degrees. Points in between two contours take on values that lie between the values of the temperature at the boundaries. Since Topeka lies about halfway between the T = 80 and T = 90 contours, we guess that the temperature in Topeka had a high of about 85 this particular day.
This type of graph is fairly common for functions of two variables. For example, a topographic map tells you the elevation (dependent variable) based on the longitude and latitude. Population density is often represented by maps similar to the temperature map above.