


Next: Exponentials
Up: Some Important Functions
Previous: Some Important Functions
Polynomials are that class of functions that are made up of several terms,
each of which is a combination of real-valued coefficients and integral
powers of the independent variable. Thus, the function 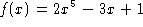 is a polynomial while the function
is a polynomial while the function 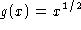 is not. Some
important things to recall about polynomials are listed below.
is not. Some
important things to recall about polynomials are listed below.
- Polynomials are continuous for all real numbers.
- The highest integral power appearing in a polynomial is called the
order or degree of the polynomial.
- It is usual to write a polynomial in standard form:
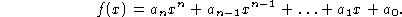
In this form, n is the degree and 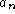 is the leading coefficient.
is the leading coefficient.
- An nth degree polynomial has at most n real roots (zeros) and
n-1 turning points, where the graph changes behavior from increasing to
decreasing or vice versa.
- The graph of a polynomial is always smooth, containing no kinks bends
or asymptotes.
Some of the most common types of polynomials are listed here.
- The polynomial
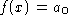 is the constant function. Its graph is a
horizontal line passing through the points where
is the constant function. Its graph is a
horizontal line passing through the points where 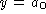 .
. - The function
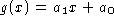 is a straight line with slope
is a straight line with slope 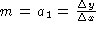 and y-intercept
and y-intercept 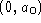 .
. - The function
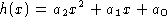 is a parabola. By
completing the square, we can rewrite the function as
is a parabola. By
completing the square, we can rewrite the function as 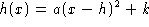 where
where 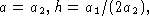 and
and 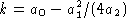 . The
vertex of the parabola is at the point (h,k) and the parabola opens
upward if a > 0, downward if a < 0.
. The
vertex of the parabola is at the point (h,k) and the parabola opens
upward if a > 0, downward if a < 0.
When graphing polynomials, it is usually a good idea to start with locating
the zeros. Since complex roots come in conjugate pairs, we know that odd
degree polynomials must have at least one real root. Often we must use a
combination of factoring, long division (or synthetic division), the
quadratic formula, and numerical techniques to locate the zeros.
It is also helpful to note the following when graphing a polynomial of
degree n and having leading coefficient 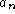 .
.
- If n is odd, then the behavior of the function (increasing or
decreasing) as
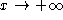 and the behavior as
and the behavior as 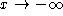 are opposite.
are opposite.
- If
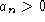 then the function ``rises to the right'' (ie. increases
as x increases.)
then the function ``rises to the right'' (ie. increases
as x increases.) - If
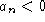 then the function ``falls to the right'' (ie. decreases
as x increases.)
then the function ``falls to the right'' (ie. decreases
as x increases.)
- If n is even, then the behavior of the function as
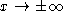 is the same.
is the same.
- If
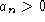 then the function rises to the right (and left.)
then the function rises to the right (and left.) - If
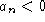 then the function falls to the right (and left.)
then the function falls to the right (and left.)



Next: Exponentials
Up: Some Important Functions
Previous: Some Important Functions
Vector Calculus
Wed Sep 17 14:50:13 MST 1997
![]() is a polynomial while the function
is a polynomial while the function ![]() is not. Some
important things to recall about polynomials are listed below.
is not. Some
important things to recall about polynomials are listed below.
![]()
![]() is the leading coefficient.
is the leading coefficient.![]() .
.