


Next: Range
Up: Definition of a Function
Previous: Notation
The domain of a function, f, can be thought of as the set of all numbers
that can legally be plugged into the function. Thus, if the domain is the
set 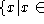 whole numbers
whole numbers 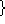 . Then the function can accept any
whole number, but if you try plugging in
. Then the function can accept any
whole number, but if you try plugging in  you never know what will
happen. In essence, the function doesn't know what to do with objects that
are not in the domain.
you never know what will
happen. In essence, the function doesn't know what to do with objects that
are not in the domain.
To find the domain, we look for a few things:
- Is the function explicitly not defined for some values of x? For
example, in the function
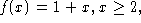 we know that we can only
plug in real numbers that are greater than or equal to 2. The most common
examples of this are the inverse trigonometric functions.
we know that we can only
plug in real numbers that are greater than or equal to 2. The most common
examples of this are the inverse trigonometric functions. - Is the function a rational function? This means that the function is
a polynomial divided by another polynomial. Since polynomials can have
zeros, if the polynomial on the bottom is zero, we are dividing by zero,
which is not allowed. Any values of x which would imply division by
zero, are implicitly outside the domain.
- More generally, does the function have any function on the bottom
which can go to zero? If so, any values which make the denominator zero
are not included in the domain. For example,
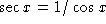 , so at
, so at 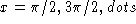 the denominator is zero and the function is
undefined.
the denominator is zero and the function is
undefined. - Are there any even roots in the function, like
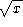 or
or
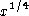 ? Since functions are usually only real valued (especially in
this course) we want to avoid values of x that make the resulting
function complex or purely imaginary.
? Since functions are usually only real valued (especially in
this course) we want to avoid values of x that make the resulting
function complex or purely imaginary. - Is there any other way the function is undefined? For example,
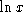 is defined only for x > 0.
is defined only for x > 0.
Vector Calculus
Wed Sep 17 14:50:13 MST 1997
![]() whole numbers
whole numbers ![]() . Then the function can accept any
whole number, but if you try plugging in
. Then the function can accept any
whole number, but if you try plugging in ![]() you never know what will
happen. In essence, the function doesn't know what to do with objects that
are not in the domain.
you never know what will
happen. In essence, the function doesn't know what to do with objects that
are not in the domain.