Hyperboloids and Cones

The hyperboloids are more interesting functions. It's actually easier to think of these as functions of three variables. Examine the function

$$G(x,y,z) = \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2}.$$

Since this is a function of three variables, we'd need four dimensional paper to draw it completely! Instead, let's try to look at level surfaces of this function. Set G(x,y,z) = k and see what we get. Each of these ``contours'' is actually a surface. The shape of this surface depends very much on what the value of k is.

If k is positive, say k = 1 we get a surface that is called a hyperboloid of one sheet. Let's assume that a, b and c are all 1. These constants only scale the surface in the x, y and z directions anyway. What we have now is the function x² + y² - z² = 1 or x² + y² = z² + 1. The contours of this surface are circles. Notice that the smallest of these circles has a radius of 1 (when z = 0.) As z gets farther from zero-in either the positive or negative direction-the circles get larger. The graph of this surface is shown below.

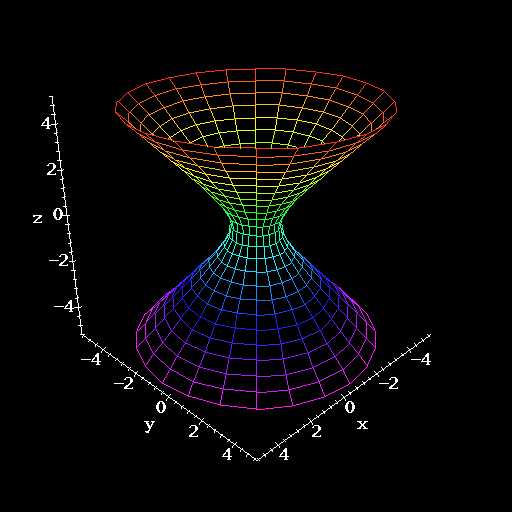
What happens if k = -1? Here, we get the function x² + y² = z² - 1. Clearly, the contours of this are circles, but notice that the circles cannot exist for |z|<1 since we need $z^2 - 1 \ge 0$. The circles for $z = \pm 1$ are simply points at the origin. This causes the surface to actually be made up of two completely separate pieces. It is called a hyperboloid of two sheets.

Now at last we come to the dividing case. Let k = 0. We are then trying to graph the surface x² + y² = z². The contours are all circular, with radii from zero on up. The sections of this function are sets of straight lines. When we put this together, we get a cone. Think of the cone as the barrier between the hyperboloid of one sheet and the hyperboloid of two sheets. If you think about it enough, you can envision the three types of surfaces fitting one inside the other, with the hyperboloid of two sheets on the inside, the hyperboloid of one sheet on the outside and the cone fitting neatly between them.

Notice that the function $z = \sqrt{x^2 + y^2}$ is the upper portion of this cone, just as the function $z = \sqrt{x^2 + y^2 + 1}$ is the upper portion of a one sheeted hyperboloid and so forth.