as 
which are the vectors in the
direction of and perpendicular to a second vector, 
.
As another example of using the dot product, consider the following
illustration. It shows how we can ``decompose'' a vector into components
along and perpendicular to a second vector. Thus, we can write the vector
as which are the vectors in the
direction of and perpendicular to a second vector, .
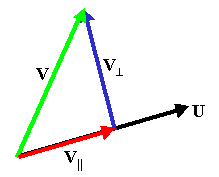
The first step is to compute 
. We can do this by using the dot
product, but we must be careful. Remember that the dot product includes the
length of both vectors. The best approach is to find a unit vector in the
direction of the second vector. This vector is simply 
.
So the length of is simply the projection of along the
unit vector. Thus,
Now, this is simply the magnitude of the part of that is
parallel to . We also need direction. But that's easy since this is
the vector parallel to , the direction of the vector must be the
direction of . So,
The other vector, the component of that is perpendicular to
can be found using the relationship 
.
You may be confused with the different ways the word ``component'' is used
throughout the subject of vector calculus. I always think of a vector as a
single object. When I want to write that vector down, I write it as being
made up of parts called components. The appearance of those components can
differ greatly depending on how one breaks the vector up. We could use good
ole' 
and so forth, or we could make reference to another vector.
As an example, let's break the vector 
into its
components parallel to and perpendicular to the vector 
.
Note that if we add the two components above we get the original vector back.