In one variable calculus, there was a simple test to determine whether a critical point was a maxima, minima, or inflection point. This second derivative test hinged on the idea of concavity-how the function was shaped at the critical point. With functions of two variables, there are now several different concavities to worry about. Is there any hope of a similar second derivative test?
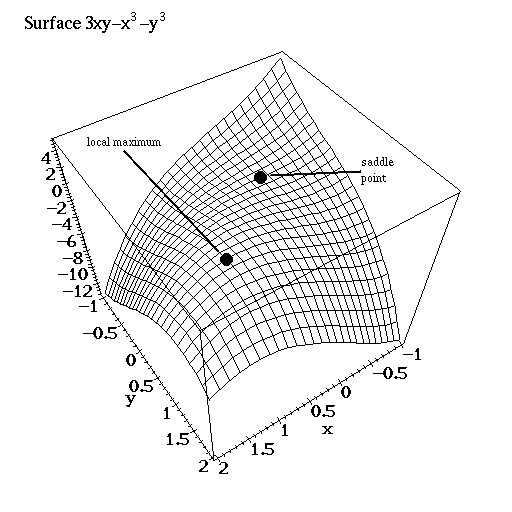
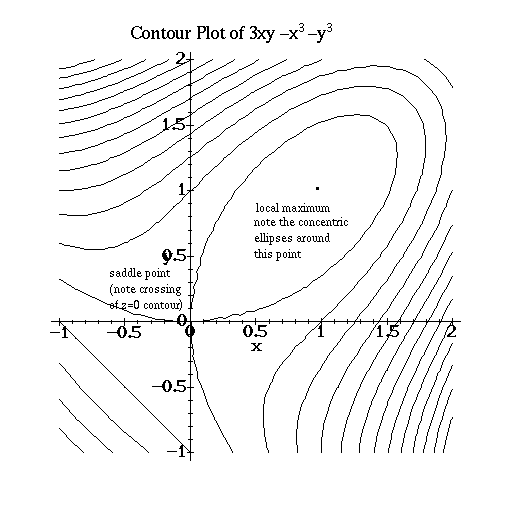
Before we decide, let's identify the type of critical points our function has the old fashioned way-looking at a graph. Once we have the location of the potential maxima and minima, we can simply graph the function or examine the contours of the function near each point.

Unfortunately, a complicated looking functions may muddy this process and prevent us from getting a clear picture. Our example is an easy case, however, since the contour diagrams clearly show (0,0) to be a saddle point and (1,1) to be a maximum.