Slope of a Section

For a start we'll look at the function z = f(x,y) one variable at a time. As you remember, this means we are looking at sections of the surface z = f(x,y) that have either x or y fixed at a constant value. Let's start by checking out the sections with x = c, so that z = f(c,y). We now have a function of one variable, y. Thus, the slope of this function at a point is known from one variable calculus to be the derivative with respect to y. In other words,

$$\mbox{slope} \thinspace = \frac{df(c,y)}{dy}.$$

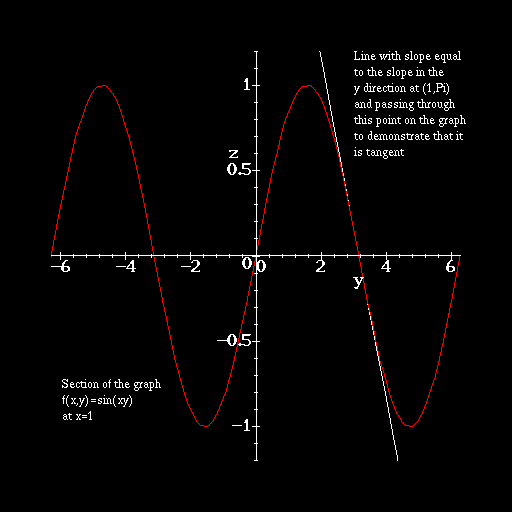
For example, if $f(x,y) = \sin(xy)$ then the slope in the y direction is simply $df(c,y)/dy = d(\sin(cy))/dy = c \cos(cy)$ by using the chain rule. Note that since x = c is fixed, we can compute the derivative just as if c were a fixed number. At the point $(1,\pi)$ the slope is -1. Graphically, this is shown below.

As another example, we can compute the slope in the x direction of z = 3x² + 2xy + 4y² at the point (1,0). The slope is

$$\frac{d}{dx}[3x^2 + 2cx + 4c^2] = 6x + 2c$$

and at the point (1,0), we have x = 1 and c = 0 so that the slope is 6.

Just as in one variable calculus, a positive slope at a point indicates that the function is increasing at that point. A negative slope indicates a decreasing function, and a zero slope indicates that the function is flat. The function above, z = 3x² + 2xy + 4y² has slope 6x + 2c in the x direction along the section y = c. Thus, for x > -c/3 the function is increasing; at x = -c/3, the function is flat; and forx < -c/3 the function is decreasing.