as 
. Now, if
we get a common denominator, we find that A(2x - 1) + B(x + 2) = x. This
equation implies that (2A + B)x = x and that -A + 2B = 0. Thus, we know
that A = 2/5 and B = 1/5. Now we can integrate the function:
Another common technique for evaluating the integral of rational functions is
to expand the fraction into a sum of simpler rational functions which can be
easily integrated. As an example of this process, let's expand the function
as . Now, if
we get a common denominator, we find that A(2x - 1) + B(x + 2) = x. This
equation implies that (2A + B)x = x and that -A + 2B = 0. Thus, we know
that A = 2/5 and B = 1/5. Now we can integrate the function:
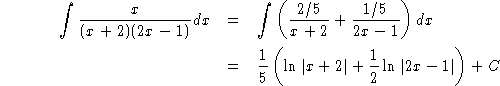
The general rule for expanding a function in partial fractions is to start with the factored form of the denominator. If none of the factors is repeated, the partial fraction expansion will be a sum of fractions, each fraction having one of the factors as its denominator. The numerator of each will be an unknown polynomial of one degree less than the denominator. For example,
Now, by getting a common denominator on the right and equating like terms in the numerators, we find that
This system can be solved to find the constants (A = 3/4, B = 0,
C = -3/4, D = 11/4) and then the first
two terms in the integral can be evaluated by substitution, and the third can
be handled by writing the fraction as 
.
The onlyreal difficulty arises in the case where one or more of the factors in the denominator is of mulitplicity k. In this case, we follow the principles of the next example.
