To evaluate an integral of the form we will use
the first of these identities. Simply let 
. Then 
and the integral becomes
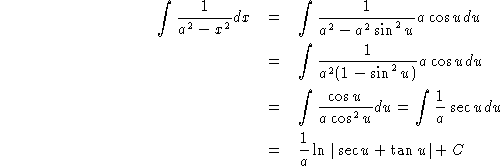
To convert this back to a function of x, we make note of the
triangle that our substitution implies. Since we let this means
that 
. This describes a right triangle with a hypotenuse of
a, an angle of u and a side of length x opposite this angle. Thus, the
other side is 
so 
and 
. Thus, the integral is evaluated to be
