


Next: Spherical Coordinates
Up: Cylindrical Coordinates
Previous: The volume element in
The center of mass of an object, W, with a density function 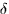 has
coordinates (xc,yc,zc) which are given by
has
coordinates (xc,yc,zc) which are given by
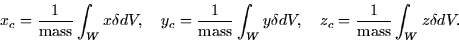
Find the center of mass of a cylindrical wedge with 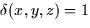 ,where the wedge W is given by
,where the wedge W is given by 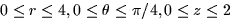 .
.
- 1.
- Calculate the total mass:
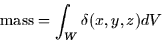
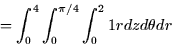
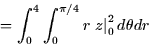
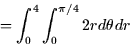
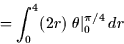
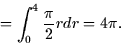
- 2.
- Next calculate xc: (Note
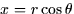 )
)
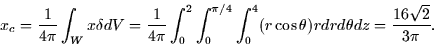
- 3.
- Calculate yc using
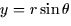 ">:
">:
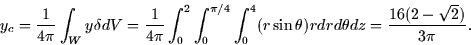
- 4.
- Calculate zc: (note z is the same in both coordinates)
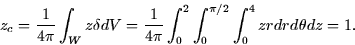
Vector Calculus
8/20/1998
![]() has
coordinates (xc,yc,zc) which are given by
has
coordinates (xc,yc,zc) which are given by
![]()
![]() ,where the wedge W is given by
,where the wedge W is given by ![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()