Cylindrical coordinates are a three dimensional version of polar
coordinates. The variables here are ![]() :
:
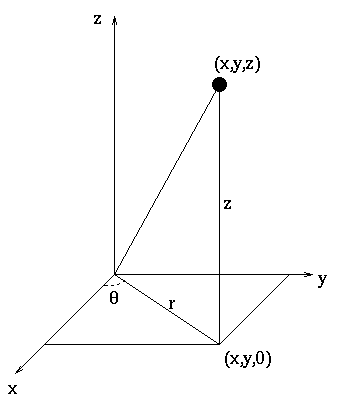
The relationship between cylindrical and Cartesian coordinates is
![]()
to convert from cylindrical to Cartesian, and
![]()
to convert from Cartesian to cylindrical. Note that this makes r the distance from the z-axis.
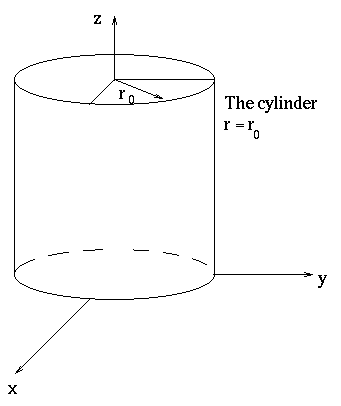
Using this, we see that r = r0 defines a cylinder of radius r0 centered on the z-axis.
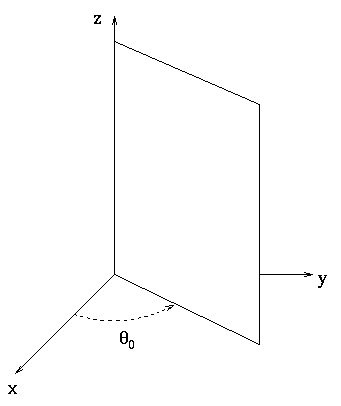
The equation ![]() defines a plane through the z-axis.
defines a plane through the z-axis.
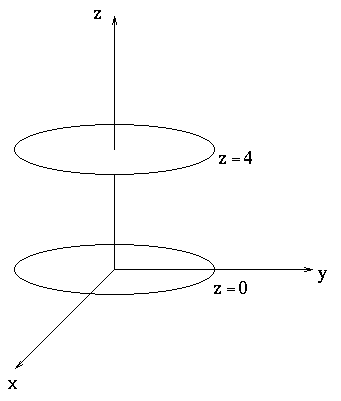
The equation z = z0 defines a plane parallel to the xy-plane, passing through the point (0,0,z0).