What is Circulation?

To state the answer to this question as easily as possible, circulation is the line integral of a vector field around a closed path. That's it. As such, it is another way to measure the amount of ``swirl'' in a vector field. Often, circulation is noted by a modified line integral:

$$\oint_C \vec{F} \cdot d\vec{r}.$$ (1)

Example 1. The circulation of the vector field $\vec{F}$around the path shown is zero. We can see this by first rewriting the circulation as a sum of line integrals along each separate piece of the curve. Thus,

$$\oint_C \vec{F} \cdot d\vec{r} = \sum_{i=1}^4 \int_{C_i} \vec{F} \cdot d\vec{r}.$$ (2)

Now, since the vector field is perpendicular to the path along C₁ and C₃, their contribution to the integral is zero. Since the magnitude of $\vec{F}$ is the same along C₂ and C₄ but they are traversed in opposite directions, we have that

$$\int_{C_2} \vec{F} \cdot d\vec{r} = - \int_{C_4} \vec{F} \cdot d\vec{r}$$ (3)

so that each of these integrals cancels the other and the total is zero.

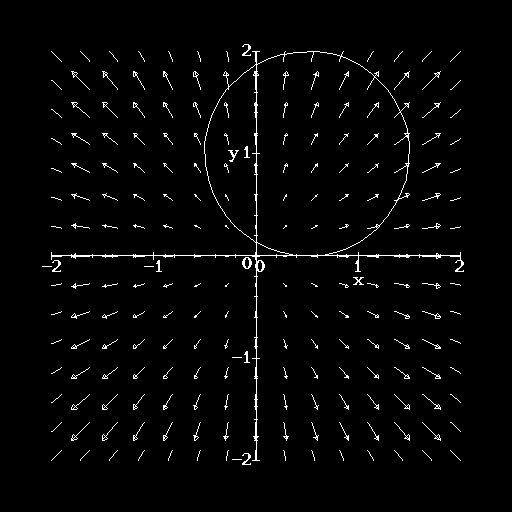
Example 2. The circulation of $\vec{G} = x^2y\hat{i} + y \hat{j}$ around the curve C shown below. This curve is broken up into three segments:

$$C_1: \quad x(t) = t, y(t) = 0 \qquad 0 \le t \le 1$$

$$C_2: x(t) = \cos t, y(t) = \sin t \qquad 0 \le t \le \pi/2$$

$$C_3: x(t) = 0, y(t) = 1 - t \qquad 0 \le t \le 1.$$

We can break the integral up into three pieces: $\oint_C \vec{G} \cdot d\vec{r} = \int_{C_1} \vec{G} \cdot d\vec{r} + \int_{C_2} \vec{G} \cdot d\vec{r} + \int_{C_3} \vec{G} \cdot d\vec{r}.$ Calculating each piece separately, we find:

$$\int_{C_1} \vec{G} \cdot d\vec{r} = \int_0^1 (0) dt = 0$$

$$\int_{C_2} \vec{G} \cdot d\vec{r} = \int_0^{\pi/2} (\cos^2t ... ...} + \sin t \hat{j}) \cdot (-\sin t \hat{i} + \cos t \hat{j}) dt$$

$$= \int_0^{\pi/2} (\cos^4 t-\cos^2 t + \frac{1}{2}\sin 2t)dt$$

$$= \left[ \frac{3t}{8} - \frac{t}{2} - \frac{1}{4} \cos 2t \right]_0^{\pi/2} = -\frac{\pi}{16} + \frac{1}{2}$$

$$\int_{C_3} \vec{G} \cdot d\vec{r} = \int_0^1 (t-1) dt = \left[ \frac{1}{2} t^2 - t \right]_0^1 = - \frac{1}{2}$$

Thus, the total circulation of $\vec{G}$ around this curve is the sum of these values, namely, $-\pi/16$.

Example 3. What about the circulation of a conservative vector field? This is obviously zero since $\vec{F} = \mbox{grad}f$ so that $\oint_C \vec{F} \cdot d \vec{r} = \oint_C \mbox{grad}f \cdot d\vec{r} = f(Q) - f(P)$ and the curve C starts and ends at the same spot (P = Q.)