along the curve C which is the straight line from the origin
to the point (1,1). One way to describe the curve C is to say it is the
graph of the equation y = x as x ranges from 0 to 1. So we can
parameterize the line as x = t, y = t, 
. Then, we see that,
along C, the vector field is 
, so
and 
where is the line segement from the origin to (1,0) and is
the line segment from (1,0) to (1,1). Along we have 
so that 
. Along we have
so that . The line
integral is then
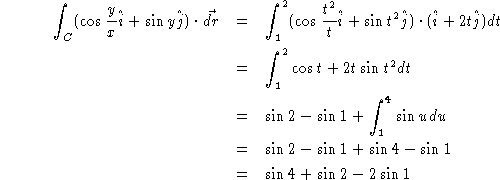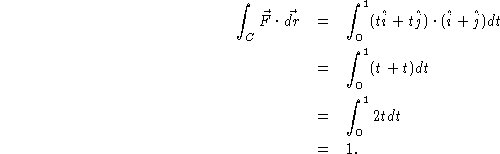
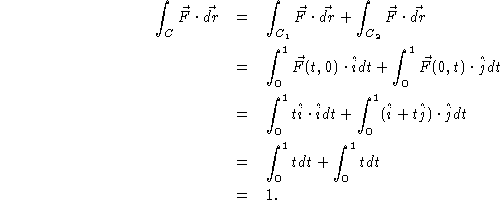
Notice that this is the same answer as in the previous example, even though we used a different path of integration. This happened because the vector field is a speacial type of vector field. The entire next chapter will be devoted to studying the interesting properties of these fields, called conservative vector fields. To see that this doesn't always work, try the integrating the vector field over the same two paths.
. Compute the line integral of this vector field
along the path 
between the points (1,1) and (2,4). The proper
parameterization of the path is 
. Then,
with 
.
