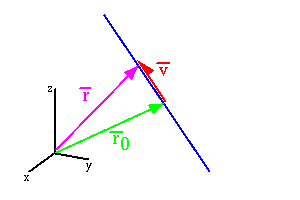
Parameterizing a striaght line requires two pieces of information:
In order to parameterize the line, we use vector addition. A
scalar multiple of ![]() still points in the same direction as
still points in the same direction as
![]() . Let the first point on the line be
. Let the first point on the line be ![]() . Another point
on the line can be obtained by adding
. Another point
on the line can be obtained by adding ![]() to
to ![]() as shown in
the figure below. If we continue to add scalar multiples of
as shown in
the figure below. If we continue to add scalar multiples of ![]() to
the initial point, we can get the whole line. By letting t be a
parameter which multiplies
to
the initial point, we can get the whole line. By letting t be a
parameter which multiplies ![]() we get the parameterization of the
line via vector addition as
we get the parameterization of the
line via vector addition as
| (15) |
Example. What is the parameterization of the line segment which starts at (1,0,5) and ends at (-4, 2, 0)?
If we let ![]() and
and ![]() , then a displacement vector that is parallel to the line would be
, then a displacement vector that is parallel to the line would be
| (16) |
So, as t ranges from 0 to 1, the parameterization
| (17) |
traces out the line segment.