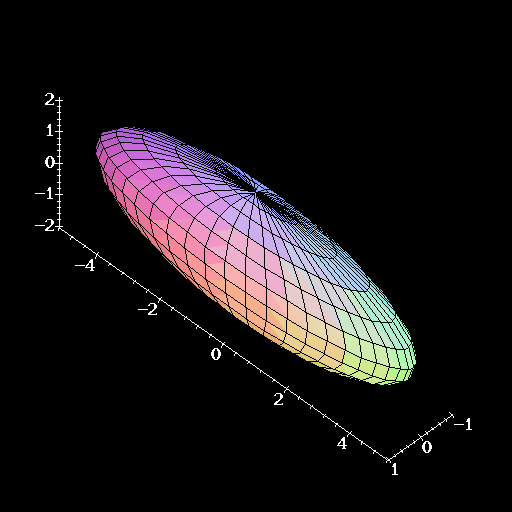We now come to another important type of function. To understand what it
looks like, we'll take a brief detour of what it means to measure distance
in three dimensions. Recall that in two dimensions, we can use the
Pythagorean theorem to calculate the distance from the point (x0, y0)
to the origin. It's simply ![]() . This is the same as
the magnitude of the position vector that points to the points (x0,
y0). In three dimensions, we can do the same thing. If a point has
coordinates (x0, y0, z0) then it has a position vector
. This is the same as
the magnitude of the position vector that points to the points (x0,
y0). In three dimensions, we can do the same thing. If a point has
coordinates (x0, y0, z0) then it has a position vector ![]() and is a distance
and is a distance ![]() from the origin.
from the origin.
Suppose we want to know what the equation of a sphere is. We can use the distance formula above to help. If the sphere is centered at the origin and has a radius of R units, then we know that the surface of the sphere is made up of every point that is exactly R units from the origin. Thus, if we let (x,y,z) be a point on the surface of the sphere, we have
![]()
For a sphere centered elsewhere, we modify the distance formula. If the center of the sphere is at (x0, y0, z0) and the sphere has a radius of R, then each point (x,y,z) on the surface is R units from the center, so
![]()
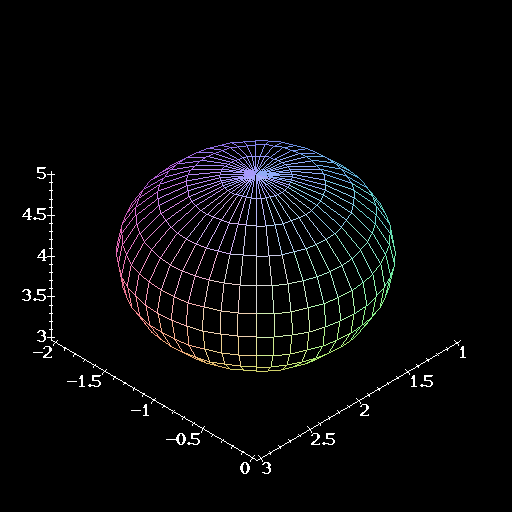
Now, let's modify the formula for the sphere centered at the origin a little. Suppose we want to draw the surface represented by
![]()
![]()