Before we can discuss the analytical approach to dealing with vectors, we need
to learn how to write them down. One method has already been mentioned. This
uses the relationship between a position vector and a point in ![]() to write a vector as an ordered n-tuple. For instance, the vector (3,-1,4)
points three units toward the x axis, one unit down the y axis,
and 4 units along the positive z axis. As we move into higher dimensions
than three, we just add more numbers to the list. So, in
to write a vector as an ordered n-tuple. For instance, the vector (3,-1,4)
points three units toward the x axis, one unit down the y axis,
and 4 units along the positive z axis. As we move into higher dimensions
than three, we just add more numbers to the list. So, in ![]() , the
vector
, the
vector ![]() is just the same as the ordered n-tuple
is just the same as the ordered n-tuple
![]() where the numbers
where the numbers ![]() are called the
components of the vector
are called the
components of the vector ![]() .
.
Another method of writing vectors involves the ideas of scalar multiplication and the addition of vectors. We start by creating a set of vectors called basis vectors. These vectors have two important properties.
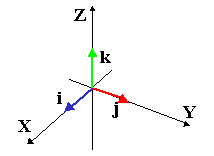
If we want a vector that points three units along the +x axis, we can simply
multiply the vector ![]() by the scalar 3 to get
by the scalar 3 to get ![]() . We can do
similar things to get the vectors in the y and z directions. Now, if we
add up these vectors, we'll have a vector which points out in some direction
determined by the components of the vector. Thus, the vector (3, -1, 4)
could be written as
. We can do
similar things to get the vectors in the y and z directions. Now, if we
add up these vectors, we'll have a vector which points out in some direction
determined by the components of the vector. Thus, the vector (3, -1, 4)
could be written as ![]() .
.