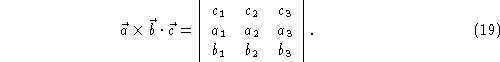The triple product

A three dimensional analogue of this is called the triple product: . Before the graphical interpretation is explained, it is worth noting that there is only one way to correctly compute this quantity. We must take the cross product first, since the cross product produces a vector which we can then dot with . If we tried to compute the dot product first, we would be left with trying to compute the cross product of a vector and a scalar, which is an undefined operation.

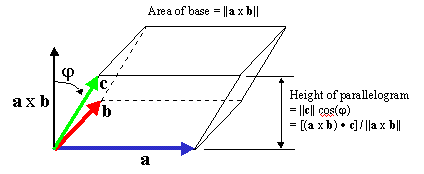
From the picture, it is clear that the area vector of the base of the parallelepiped is . Since this vector forms an angle with the thrid vector, the volume of the figure is simply the base times the perpendicular height, .

This is the result of the triple product which can also be written in matrix notation as