Now suppose we want to calculate the flux of ![]() through S where
S is a piece of a sphere of radius R centered at the origin. The
surface area element (from the illustration) is
through S where
S is a piece of a sphere of radius R centered at the origin. The
surface area element (from the illustration) is
![]()
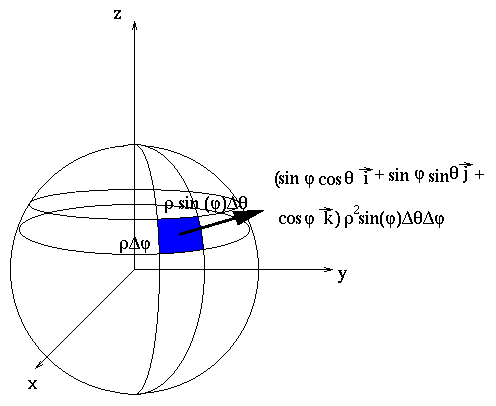
The outward normal vector should be a unit vector pointing directly away
from the origin, so (using ![]() and
spherical coordinates) we find
and
spherical coordinates) we find
![]()
![]()
![]()
As an example, let's compute the flux of ![]() through S, the upper hemisphere of radius 2 centered at the origin,
oriented outward.
through S, the upper hemisphere of radius 2 centered at the origin,
oriented outward.
![]()
![]()
![]()
![]()
![]()