Average value of a function

To find the average value of a function of two variables, let's start by looking at the average value of a function of one variable. Note that, over the interval $a \le x \le b$, the integral $\int_a^b f(x)dx$ gives the total area of the region. We could also get the total area of the region by treating the region as a rectangle of length b-a and height equal to the average value of the function.

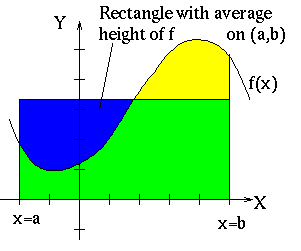
Thus,

$$(\mbox{average value of $f$})(b-a) = \int_a^b f(x)dx.$$

Rearranging this formula, we see that

$$\mbox{Average value of $f$} = \frac{1}{b-a}\int_a^b f(x)dx.$$

We can perform a similar ``trick'' for functions of two variables. The volume under f is given by $\int_R fdA$. But we could treat this volume as a solid whose cross section is shaped like R and whose height is the average value of f over the region R:

$$(\mbox{average of $f$\space over $R$})(\mbox{area of $R$}) = \int_R fdA \Rightarrow$$

$$\mbox{Average of $f$} = \frac{1}{\mbox{Area of $R$}}\int_R fdA.$$

To envision this, think of building the volume under z=f(x,y) as a solid mass of wax. Trap the wax inside a tube whose cross-section looks like R. As the wax melts, it will eventually form a solid whose height is equal to the average value of f on the region R.

Click here to view an animation of a function made of wax melting to its average value. This will open a new window. To return to this window, simply close the new one. To view the animation repeatedly, use the "reload" feature of your browser.

How do we calculate the area of a region? The area of a region R will be the same as the integral of a uniform density of 1 over the region. Thus,

$$\mbox{Area of $R$} = \int_R 1 dA = \int_R dA.$$