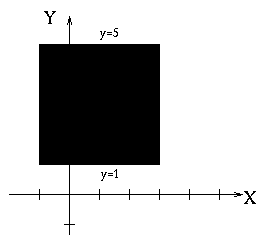
The reason that we must be careful evaluating integrals over a general
region is simple. For a rectangular, the boundaries of the region (limits
of integration) are all described by constant functions. For
example, the region below has these boundaries:
| Boundary | Equation |
|---|---|
| left | x = -1 |
| right | x = 3 |
| bottom | y = 1 |
| top | y = 5 |
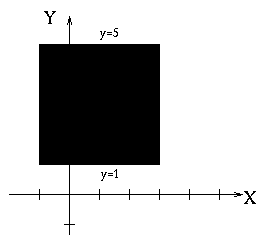
Thus, the limits of integration in each of the iterated integrals are constants. What about the boundaries of the region below?
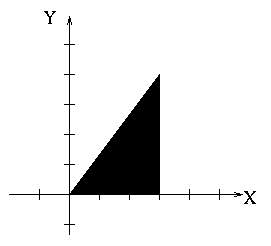
The boundaries are
| Boundary | Equation |
|---|---|
| left | x = 0 |
| right | x = 3 |
| bottom | y = 0 |
| top | y = 4x/3 |
or, the boundaries could be described as
| Boundary | Equation |
|---|---|
| left | x = 3y/4 |
| right | x = 3 |
| bottom | y = 0 |
| top | y = 4 |
The choice of which set of boundaries we use (they both describe the same region) influences the order of integration and vice versa.