Some functions won't work one way

$next$ $up$ $previous$
Next: More on breaking up Up: The Order of Integration Previous: The shape of a

Some functions won't work one way

Some functions are difficult (if not impossible) to integrate in a particular order over some regions. For example, let's try to evaluate

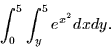
$\begin{displaymath} \int_0^5 \int_y^5 e^{x^2} dx dy.\end{displaymath}$

To integrate in the order given, we need to evaluate $\int e^{x^2} dx$ .This cannot be done. Ever. Thus, we have no choice but to attempt reversing the order of integration.

1.

First, determine the boundaries of the region. As given in the integral, we have

Boundary	Equation
left	x = y
right	x = 5
bottom	y = 0
top	y = 5

2.

Next, we should draw the region.

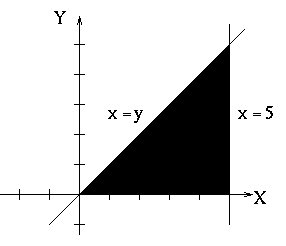
3.

Find the bottom and top boundaries. The bottom is just y = 0. The top is the line y = x.

4.

Find the left and right boundaries. The left is just x = 0 and the right is x = 5.

5.

Now we set up the integral and evaluate it.

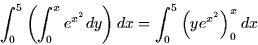
$\begin{displaymath} \int_0^5 \left( \int_0^x e^{x^2} dy \right) dx = \int_0^5 \left( ye^{x^2} \right)_0^x dx \end{displaymath}$

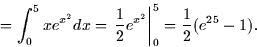
$\begin{displaymath} = \int_0^5 xe^{x^2} dx = \left. \frac{1}{2} e^{x^2} \right\vert _0^5 = \frac{1}{2} (e^{25} - 1).\end{displaymath}$

The clue that you need to switch the order of integration is the is you switch it, you get an integrating factor which lets you evaluate the outer integral by substitution.

$next$ $up$ $previous$
Next: More on breaking up Up: The Order of Integration Previous: The shape of a

Vector Calculus
8/20/1998
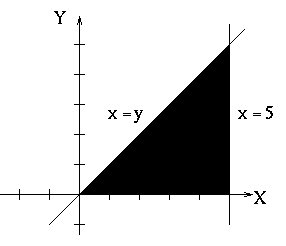