Return to section 5 information/
Return to current instructors/
Return to main menu.
Computer Use Assignment
Kris Green: Math 223, Section 2
Fall 1998: Due Friday, August 28
The following function shows up in celestial mechanics:
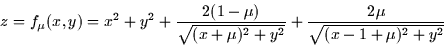
where  is a parameter that is fixed. The physical situation (not
necessary for working the problem) is that a large mass, say the earth, is
located at
is a parameter that is fixed. The physical situation (not
necessary for working the problem) is that a large mass, say the earth, is
located at 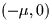 and a smaller mass, say the moon, at
and a smaller mass, say the moon, at  .The coordinates are chosen so that the center of mass of the two objects is
at (0,0) and the coordinates rotate around the center of mass at the proper
rate. The function then gives the set of points where a third mass that is
very small (say a satellite) would have zero orbital velocity. The
function is used to find stable orbits for various situations.
.The coordinates are chosen so that the center of mass of the two objects is
at (0,0) and the coordinates rotate around the center of mass at the proper
rate. The function then gives the set of points where a third mass that is
very small (say a satellite) would have zero orbital velocity. The
function is used to find stable orbits for various situations.
The Problem: Start with 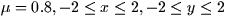 and choose
and choose 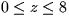 to view the function above in WinPlot. Note
that this function is way too complicated to visualize without some sort of
help.
to view the function above in WinPlot. Note
that this function is way too complicated to visualize without some sort of
help.
- 1.
- Look at the surface from a few different viewpoints. Try to
describe, in words, what you see.
- 2.
- Use WinPlot (under ``Mode'') to plot the level curves of the
function. (At some point, you'll have to press ``Q'' to stop the plot.)
Sketch these level curves. Be sure to include some values for the function
along a few of the curves. You can print the level curves that the program
generates, but make sure to add labels, by right clicking on the location
and typing the text in.
- 3.
- Does the computer accurately show the graph of
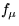 near the
points
near the
points  and
and 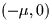 ? Why or why not? [Hint: look at the
algeraic form of the function.]
? Why or why not? [Hint: look at the
algeraic form of the function.]
- 4.
- What effect does changing
 have on the surface? [For example,
try
have on the surface? [For example,
try 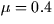 or 0.2.]
or 0.2.]
Getting Help: I will hold my office hours in Math 226 (the open
access computer lab) for the rest of the week. This should allow you
sufficient time to play with WinPlot and get an idea of what it can do for
you.
Vector Calculus
9/10/1998
![]()
![]() and choose
and choose ![]() to view the function above in WinPlot. Note
that this function is way too complicated to visualize without some sort of
help.
to view the function above in WinPlot. Note
that this function is way too complicated to visualize without some sort of
help.