Computer Project
Math 223, Section 5, Spring 1999
Instructions: This project will rely heavily on using some
computer-aided graphics
package (like WinPlot, available in the open access lab, Math 226.) I
encourage you to work with others on this project, but each of you must
turn in your own work. This will be a graded homework assignment. Answer
all questions in complete sentences. You may wish to use a graph or
equation to support your statements, but do not simply write the equations
out in words. Do not underestimate this project. You will need to spend
some time on it. Your final report should be two to three pages long.
Consider the following function of two variables:
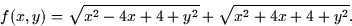
- 1.
- Describe the shape of the surface which represents this function.
Are there any symmetries? If so, be sure to both describe them and show
them analytically on paper.
- 2.
- What shape are the sections of the surface plot of f? Does the
shape of the sections change (eg. are some parabolas? lines? sine curves?)
- 3.
- What shape are the contours? Do any contours cross? Do any contours
not have the same basic shape as the others? If so, which ones?
- 4.
- Given that the distance between the point (x,y) and the point
(a,b) is
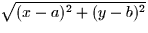 , what does the function f(x,y)
represent? How does this explain part (3)? (Hint: what is the definition
of an ellipse?)
, what does the function f(x,y)
represent? How does this explain part (3)? (Hint: what is the definition
of an ellipse?)
- 5.
- Suppose the plane z = ny + d intersects the graph of f so that
the intersection forms a circle. How might one choose n and d in order
to insure that this happens? You may find it easier to describe the process
rather than find actual values.
A trick you might find useful during this project is completing the
squares. This involves rewriting the expression ax2 + bx + c:
You may find it easier to simply factor some of the expressions you meet
during this project. Remember, if you have any trouble, email me (
kgreen@math.arizona.edu) or come by my office.
Vector Calculus
1/20/1999
![]()