In this project,
you will explore various topics dealing with derivatives of multivariable
functions. You will be given several functions of two variables and
several points on these functions. Your task will be to construct the
tangent plane to the function at each of these points, then graph the
function and all of the tangent planes that you found on the same set of
axes. For example, if you were given the paraboloid z = f(x,y) = x^2 + y^2
and the points (0,0) and (1,3) you could compute that the tangent plane at
(0,0) is z = f(0,0) + fx(0,0) (x-0) + fy(0,0) (y-0) =
0; the tangent plane at (1,3) is z = 2(x-1) + 6(y-3) + 10. The graph would
then look like the plot below.
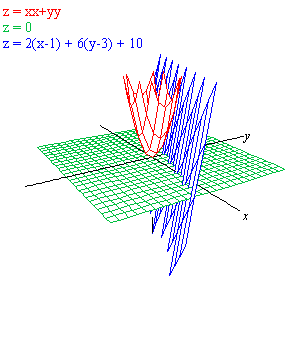 Note that the
planes are shown and that they are indeed tangent to the
surface of the function at the indicated points. You may have to play
around with the view point (using F8, CRTL-F8, F9, and CTRL-F9) as well as
the setting for the ranges of x and y in order to fit the planes on one
picture. Note the program Winplot will allow you to place the equations of
each of the objects graphed onto the plot (in the upper left hand corner of
the plot.) This is done by selecting the equation you wish to display in
the "inventory" window and clicking on the "equa"
button. Do this for each plane and each surface. Also note that the edges
of the surface and planes will look ragged. This is not the way the
"real" surface or plane look. It is merely an artifact of
graphing the equations on a fixed domain of (x,y) points. The computer
creates a table and connects the dots to make the pictures. Make these
sorts of graphs for each of the following functions and the points given
(which are different for each function.) Try to save paper by copying the
pictures to the clipboard as bitmaps (using the "file" menu) and
then pasting them onto a single page or two page document in Microsoft Word
or some other word processor. When you are done, go back to the graphs
with a pencil and draw the vectors which are normal to the surface at each
of the points where you found the tangent plane. Note that you know the
vectors since you have the equations of the planes. What is the general
formula for the normal vector to the surface z = f(x,y) at the point
(a,b,f(a,b))?
Note that the
planes are shown and that they are indeed tangent to the
surface of the function at the indicated points. You may have to play
around with the view point (using F8, CRTL-F8, F9, and CTRL-F9) as well as
the setting for the ranges of x and y in order to fit the planes on one
picture. Note the program Winplot will allow you to place the equations of
each of the objects graphed onto the plot (in the upper left hand corner of
the plot.) This is done by selecting the equation you wish to display in
the "inventory" window and clicking on the "equa"
button. Do this for each plane and each surface. Also note that the edges
of the surface and planes will look ragged. This is not the way the
"real" surface or plane look. It is merely an artifact of
graphing the equations on a fixed domain of (x,y) points. The computer
creates a table and connects the dots to make the pictures. Make these
sorts of graphs for each of the following functions and the points given
(which are different for each function.) Try to save paper by copying the
pictures to the clipboard as bitmaps (using the "file" menu) and
then pasting them onto a single page or two page document in Microsoft Word
or some other word processor. When you are done, go back to the graphs
with a pencil and draw the vectors which are normal to the surface at each
of the points where you found the tangent plane. Note that you know the
vectors since you have the equations of the planes. What is the general
formula for the normal vector to the surface z = f(x,y) at the point
(a,b,f(a,b))?
- f(x,y) = exp(-x^2-y^2) at the points (0,0), (1,1), and (-3,-2)
- f(x,y) = sin(y) at the points (0,0), (2,pi/2), and (5,pi/4)
- f(x,y) = (x+y)/(x-y) at the points (2,5) and (5,2)
 Note that the
planes are shown and that they are indeed tangent to the
surface of the function at the indicated points. You may have to play
around with the view point (using F8, CRTL-F8, F9, and CTRL-F9) as well as
the setting for the ranges of x and y in order to fit the planes on one
picture. Note the program Winplot will allow you to place the equations of
each of the objects graphed onto the plot (in the upper left hand corner of
the plot.) This is done by selecting the equation you wish to display in
the "inventory" window and clicking on the "equa"
button. Do this for each plane and each surface. Also note that the edges
of the surface and planes will look ragged. This is not the way the
"real" surface or plane look. It is merely an artifact of
graphing the equations on a fixed domain of (x,y) points. The computer
creates a table and connects the dots to make the pictures. Make these
sorts of graphs for each of the following functions and the points given
(which are different for each function.) Try to save paper by copying the
pictures to the clipboard as bitmaps (using the "file" menu) and
then pasting them onto a single page or two page document in Microsoft Word
or some other word processor. When you are done, go back to the graphs
with a pencil and draw the vectors which are normal to the surface at each
of the points where you found the tangent plane. Note that you know the
vectors since you have the equations of the planes. What is the general
formula for the normal vector to the surface z = f(x,y) at the point
(a,b,f(a,b))?
Note that the
planes are shown and that they are indeed tangent to the
surface of the function at the indicated points. You may have to play
around with the view point (using F8, CRTL-F8, F9, and CTRL-F9) as well as
the setting for the ranges of x and y in order to fit the planes on one
picture. Note the program Winplot will allow you to place the equations of
each of the objects graphed onto the plot (in the upper left hand corner of
the plot.) This is done by selecting the equation you wish to display in
the "inventory" window and clicking on the "equa"
button. Do this for each plane and each surface. Also note that the edges
of the surface and planes will look ragged. This is not the way the
"real" surface or plane look. It is merely an artifact of
graphing the equations on a fixed domain of (x,y) points. The computer
creates a table and connects the dots to make the pictures. Make these
sorts of graphs for each of the following functions and the points given
(which are different for each function.) Try to save paper by copying the
pictures to the clipboard as bitmaps (using the "file" menu) and
then pasting them onto a single page or two page document in Microsoft Word
or some other word processor. When you are done, go back to the graphs
with a pencil and draw the vectors which are normal to the surface at each
of the points where you found the tangent plane. Note that you know the
vectors since you have the equations of the planes. What is the general
formula for the normal vector to the surface z = f(x,y) at the point
(a,b,f(a,b))?