
Coordinate Systems and Formulae
Cartesian Coordinates
![]()
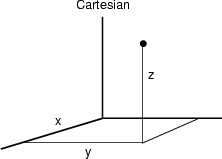
![]()
![]()
![]()
![]()
Cylindrical Coordinates
![]()
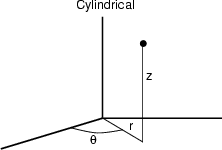
![]()
![]()
![]()
![]()
![]()
Spherical Coordinates
![]()
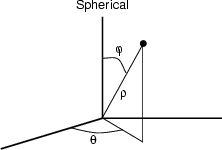
![]()
![]()
![]()
![]()
![]()
![]()
Formulae Involving The Del Operator
If ![]() and
and ![]() are smooth vector fields and
are smooth vector fields and ![]() and
and ![]() are smooth scalar functions of position (x,y,z) then
are smooth scalar functions of position (x,y,z) then
- 1.
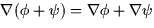
- 2.
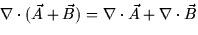
- 3.
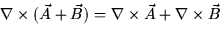
- 4.
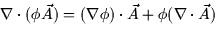
- 5.
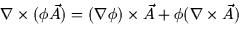
- 6.
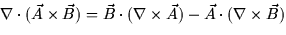
- 7.
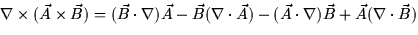
- 8.
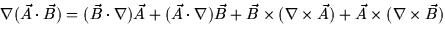
- 9.
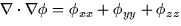 , in
Cartesian coordinates
, in
Cartesian coordinates
- 10.
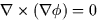
- 11.
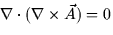
- 12.
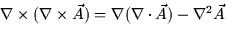
The Vector Calculus Website at
http://www.math.arizona.edu/~vector