
Summary of Math 223
Mathematical objects we have met
- 1.
- Scalar variables: These are variables which hold a single value, such as x, y, or t.
- 2.
- Vector variables (Chapter 12): These are variables which store several
pieces of information and are denoted by
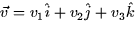 (in three space) or
(in three space) or 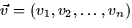 (in
n dimensional space.)
(in
n dimensional space.)
- 3.
- Scalar fields (Chapter 11): These are also referred to as functions. An object such as f(x,y,z) assigns a single scalar value to each point (x,y,z) in the domain of f.
- 4.
- Vector fields (17.1): A vector field such as
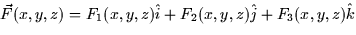 assigns a vector
to each point in the domain.
assigns a vector
to each point in the domain.
- 5.
- Parameterized curves (16.1): A curve is a one dimensional object and
can be described by a single parameter, such as t. To describe a curve,
simply specify x = x(t), y = y(t), z = z(t) together with a range of
values for t (such as
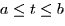 .) Optionally, one can use the
position vector,
.) Optionally, one can use the
position vector,  .
. - 6.
- Parameterized surfaces: see section 16.3
- 7.
- The del operator (13.4-5, 20.1, 20.3): (also called nabla) is the operator
 . It has no meaning by itself and must
be used to operate on other objects.
. It has no meaning by itself and must
be used to operate on other objects.
Derivative operations on these objects
Scalar fields: For a scalar field f(x,y,z) we have
- 1.
- Partial derviatives (13.1-2, 13.5):
 denotes the rate of change of f in the x-direction, similar derivatives
exist for the y and z directions;
denotes the rate of change of f in the x-direction, similar derivatives
exist for the y and z directions;
- 2.
- Higher partial derivatives (13.7): since the partial derivatives are functions, they too have derivatives; if the function is smooth, then mixed partials are equal (ie. fxy = fyx, fxzz = fzxz = fzzx;)
- 3.
- Gradients (13.4-5): grad
 . At each point, grad f tells you which direction f is
increasing the most, as well as the rate of increase in that direction;
. At each point, grad f tells you which direction f is
increasing the most, as well as the rate of increase in that direction;
- 4.
- Directional derivative (13.4-5): the rate of change of a function f
in the direction of the unit vector
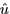 is
is 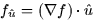 ;
; - 5.
- Laplacian (??): the Laplacian of a scalar field is simply
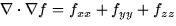 .
.
Vector fields
- 1.
- Divergence (20.1): The divergence of a vector field measures the flux
density at a point. It is represented by div
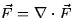 which is defined to be
which is defined to be
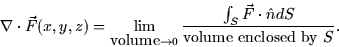
- 2.
- Curl (20.3): The curl of a vector field is a vector that points in the
direction perpendicular to the plan of maximum circulation density and has
magnitude equal to this maximum circulation density. In other words, it
points in the direction in which
is the greatest.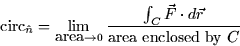
Parameterized curves: For a curve 
- 1.
- Velocity (16.2): The velocity vector,
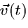 , points tangent to the
path, and is simply
, points tangent to the
path, and is simply 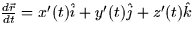 .
. - 2.
- Speed (16.2): This is the magnitude of the velocity vector,
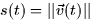 .
. - 3.
- Acceleration (16.2): this measures the change in the velocity vector;
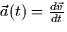 .
. - 4.
- Distance along the curve (16.2): if the path never crosses itself and there
is no value of t for which
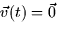 then the distance
along the curve from t = a to t = b is
then the distance
along the curve from t = a to t = b is 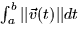 .
.
Integral operations on these objects
Scalar fields
- 1.
- The volume beneath the surface f(x,y) that lies
above the region R (15.1)
in the xy-plane is
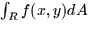 where dA is the area element in
the coordinate system. In Cartesian, dA = dx dy. In polar
(15.5),
where dA is the area element in
the coordinate system. In Cartesian, dA = dx dy. In polar
(15.5), 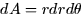 . This is usually expressed as an iterated integral (15.2), for
example:
. This is usually expressed as an iterated integral (15.2), for
example:

- 2.
- Triple integrals (15.3): these are simply a further extension of double
integrals. For an interpretion, let W be a three dimensional volume
over which the mass density of an object,
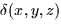 is defined. Then
is defined. Then
where dV is the appropriate volume element. In Cartesian, dV = dx dy dz. In cylindrical (15.6),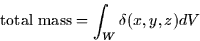
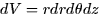 . In spherical (15.6),
. In spherical (15.6), 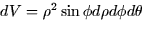 .
. - 3.
- Averages: the average value of f(x,y) over the region R is
If the function is defined over a three dimensional region W then the average of f over this region is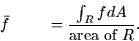
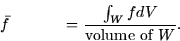
- 4.
- Area of a region: the total area of R is simply
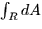 .
. - 5.
- Volume: the total volume of a region W is
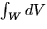 .
.
Vector fields
- 1.
- Line integrals (18.1-2): These measure the amount of work which a vector
field ``does'' along a curve. If the curve, C, is parameterized by
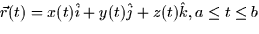 then
then
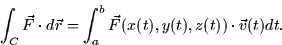
- 2.
- Flux integrals (19.1-2): These measure how much a vector field flows through
an oriented surface. If the surface, S, is given by z = f(x,y) and lies
above a region R (this is the shadow of S) in the xy-plane then
if the surface is oriented upwards (towards +z axis.)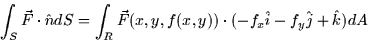
Optimization
Location of critical points (14.1)
A point P is said to be a critical point of the function f(x,y,z) if either
- 1.
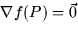 (ie. fx(P) = fy(P) = fz(P) = 0), or
(ie. fx(P) = fy(P) = fz(P) = 0), or
- 2.
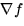 fails to exist at point P.
fails to exist at point P.
Classification of critical points (14.2)
Critical points come in three types. Maxima, minima, and saddle points.
- 1.
- A point P is a local maximum of f if f(x,y,z) < f(P) for all (x,y,z) near P.
- 2.
- A point P is a local minimum of f if f(x,y,z) > f(P) for all (x,y,z) near P.
- 3.
- A point P is a saddle point of f if there exist points Q and Q' near P such that f(P) > f(Q) and f(P) < f(Q').
- 1.
- D > 0, fxx < 0 then P is a local maximum,
- 2.
- D > 0, fxx > 0 then P is a local minimum,
- 3.
- D = 0 then P is a saddle point,
- 4.
- D < 0 then the second derivative test provides no information.
Constrained optimization (14.3)
Here we seek to find the maximum or minimum of some function f(x,y,z)
subject to the constraint that g(x,y,z) = c. This will occur at
solutions ![]() of the Lagrange multiplier problem
of the Lagrange multiplier problem
![]()
![]()
Special vector fields
Conservative and gradient fields (18.3)
A vector field ![]() is conservative if any of the following conditions
are met:
is conservative if any of the following conditions
are met:
- 1.
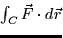 is independent of path,
is independent of path,
- 2.
- the circulation of
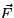 around every closed path is zero,
around every closed path is zero,
- 3.
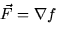 for some scalar potential function f(x,y,z).
for some scalar potential function f(x,y,z).
- 1.
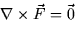 , and
, and
- 2.
- the domain,D, of
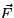 is such that any closed curve that lies
in D can be smoothly contracted to a point while always remaining inside
D,
is such that any closed curve that lies
in D can be smoothly contracted to a point while always remaining inside
D,
Curl fields (20.3, 20.5)
A vector field ![]() is said to be a curl field if
is said to be a curl field if ![]() for some vector potential
for some vector potential ![]() . The divergence test
can help determine if
. The divergence test
can help determine if ![]() is a curl field. If
is a curl field. If ![]() is a smooth
vector field in three-space and
is a smooth
vector field in three-space and
- 1.
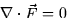 , and
, and
- 2.
- the domain, D, of
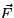 is such that every closed surface in
D encloses only points that also lie in D,
is such that every closed surface in
D encloses only points that also lie in D,
Integral theorems
Fundamental Theorem of Calculus for Line Integrals (18.4)
If C is a piecewise smooth oriented path from P to Q and f(x,y,z) is a function whose gradient is continuous on C then
![]()
Divergence Theorem (20.2)
If W is a solid region whose boundary S is piecewise smooth and
oriented outward and ![]() is a smooth vector field defined over all of
S and W then
is a smooth vector field defined over all of
S and W then
![]()
Green's Theorem (18.4)
If C is a simple closed curve surrounding a region R in the plane,
oriented so that R is always on the left as you traverse C and ![]() is smooth and defined over all of R and C
then
is smooth and defined over all of R and C
then
![]()
Stokes' Theorem (20.4)
If S is a smooth oriented surface with a piecewise smooth boundary C
oriented (from the orientation of S) by the right-hand rule and ![]() is a smooth vector field defined over all of S and C then
is a smooth vector field defined over all of S and C then
![]()
Copyright © 1998 by Kris H. Green
The Vector Calculus Website at
http://www.math.arizona.edu/~vector