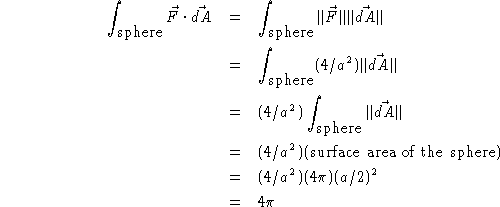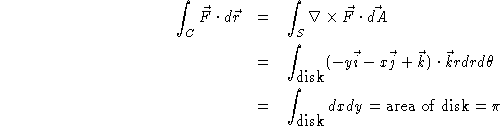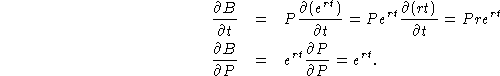
The interpretation of ![]() is to give the rate of change of
the amount in the account (B) over time. Hopefully, this is an increasing
function. The other partial derivative,
is to give the rate of change of
the amount in the account (B) over time. Hopefully, this is an increasing
function. The other partial derivative, ![]() tells you
how much the amount of money in the bank will increase as you adjust the
principal amount invested.
tells you
how much the amount of money in the bank will increase as you adjust the
principal amount invested.
- To find a normal vector to the surface S we compute the gradient of the
function g(x,y,z) = z - f(x,y) at the point indicated. So,
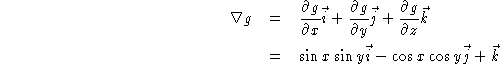
At the point
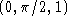 we have the normal vector as
we have the normal vector as 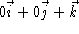 .
. - To find the tangent plane to S at this point, we use the normal
vector to find that ax + by + cz = d where a, b, and c are the
 ,
, 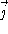 , and
, and 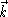 components of the normal vector and d
is a constant that is obtained by plugging in the point
components of the normal vector and d
is a constant that is obtained by plugging in the point 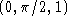 .
Thus, the tangent plane is z = 1.
.
Thus, the tangent plane is z = 1.
- For this integral, we are at values of z that are less than 1,
since we are inside a the upper hemisphere of a sphere of radius 1. This means
that the quantity
 is always negative. Since we are integrating a
negative function over a volume, we expect the result to be negative.
is always negative. Since we are integrating a
negative function over a volume, we expect the result to be negative. - The function (-xz) is an odd function of the variable x. Thus, when x is positive (the right half of the hemisphere) the integral gives a negative value (since -x is negative and z is always positive), and when x is negative, we get a positive value. Thus, the integral over the right half of the hemisphere will cancel with the integral over the left half, giving a net result of zero.
![]()
Thus, the parameterization satisfies both equations and must therefore represent a curve on each surface. Since the equations represent two different planes, and the curve that is parameterized is a straight line, this line must represent the intersection of the two planes.
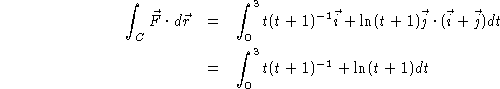
This is a difficult integral to do, but the problem is simplified by
using the Fundamental Theorem of Calculus for Line Integrals. Note that the
vector field above is a gradient field ( ![]() ) with a potential function given by
) with a potential function given by
![]() . This means that
. This means that
![]()
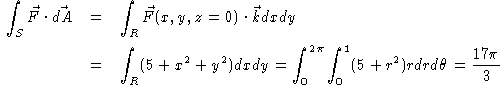
- To check whether
 is a conservative vector field (ie. has a
potential function), we calculate the curl. A simple calculation reveals that
is a conservative vector field (ie. has a
potential function), we calculate the curl. A simple calculation reveals that
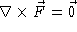 , so
, so  is a gradient field. We now
try to find a potential function by setting
is a gradient field. We now
try to find a potential function by setting 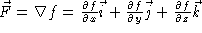 . This means that
. This means that
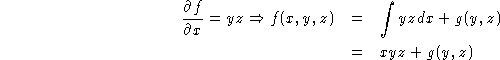
we now take partial derivatives with respect to y and compare with the second component of the vector field.
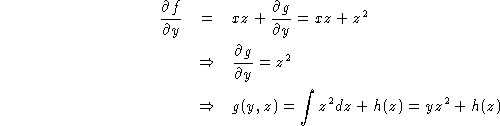
This means that we now have
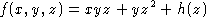 . Taking the partial
derivative of this with respect to z and comparing with the thrid component
of the vector field we find
. Taking the partial
derivative of this with respect to z and comparing with the thrid component
of the vector field we find
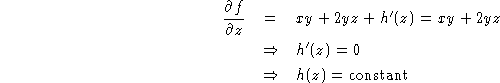
And so we find that the potential function is
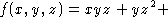 constant.
constant. - Since the vector field
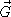 is only a two-dimensional vector field,
we can check the simpler relations to determine whether it is conservative.
We see that, letting
is only a two-dimensional vector field,
we can check the simpler relations to determine whether it is conservative.
We see that, letting 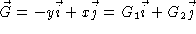 ,
,

Since these partial derivatives are not equal, we know that
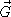 is not
a gradient field and therefore has no potential.
is not
a gradient field and therefore has no potential.
- To find the divergence of
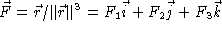 , we first write the vector field using x, y
and z and then compute div(
, we first write the vector field using x, y
and z and then compute div(  )
) 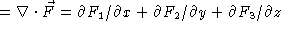 . So
. So

Now we compute the partial derivatives. For simplicity, I show only the first term,
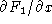 .
.
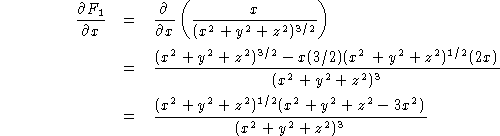
Similar terms arise from the other derivatives. In the end, you will find that div
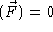 , as long as
, as long as 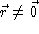 .
. - Because the divergence of this vector field is undefined at the origin,
we cannot use the divergence theorem directly to compute the flux through a
cube centered at the origin. However, we can break the region of integration
up into two pieces.
Since the vector field is pointing radially outward, it will be easy to calculate the flux through a sphere centered at the origin. For this reason, we break the cube up into two parts. The first part is the sphere, centered at the origin, with radius a/2. The second part of the region will be the cube minus the sphere. Thus, together, these regions add up to the original cube. The benefit of this approach will soon be apparent.
Through the second region (cube minus sphere) we know that the divergence of the vector field is zero. Also, since we have removed the origin (it's part of the sphere) we can use the divergence theorem. This means that the flux through the surface of region two is zero.
Through the first region, we will have to compute the flux integral. This is easy, because the vector field and the normal to the sphere are in the same direction. Furthermore, on the surface of the sphere, r = a/2, so we know
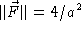 . Thus,
. Thus,