Fall 1997
Final Exam
Main menu /
Final Exams /
- 1.
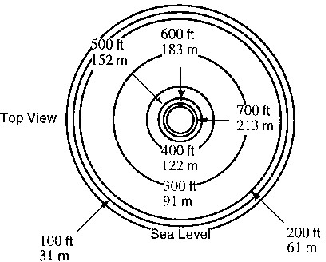
- The diagram in the figure below shows the contour map for a circular
island. Sketch the vertical cross-section of the island through the
center. Your sketch should show concavity clearly.
- 2.
- Let
 and
and 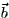 be any two nonzero vectors in 3-space,
which are not parallel to one another. Write expressions for vectors
representing the following:
be any two nonzero vectors in 3-space,
which are not parallel to one another. Write expressions for vectors
representing the following:
- (a)
- A unit vector parallel to
 .
. - (b)
- A vector perpendicular to
 and
and 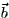 .
. - (c)
- What is the value of
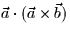 ?
Why?
?
Why?
- 3.
- In an electric circuit, two resistances, R1 and R2, are hooked
up so that their combined resistance, R, is given by R = 1/R1 + 1/R2.
- (a)
- Find
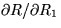 .
. - (b)
- Suppose
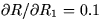 for some values of R1
and R2. What does this tell you, in terms of resistances?
for some values of R1
and R2. What does this tell you, in terms of resistances?
- 4.
- Suppose that T(x,y) = x2 + 2y2 - x is the temperature at the
point (x,y). If you are standing at the point (-2,1) and decide to
proceed in the direction of the point (1,-3), will the temperature be
increasing or decreasing at the moment you begin?
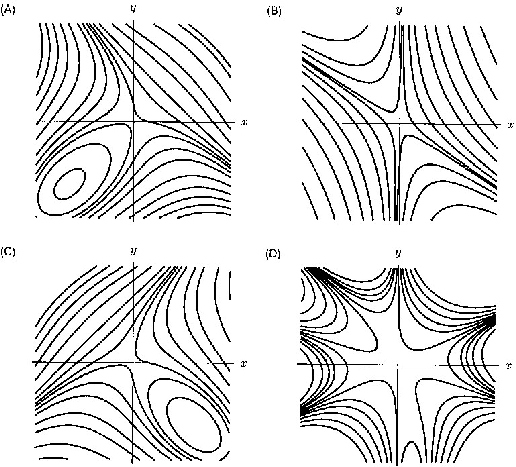
- 5.
- Let
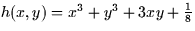 .
.
- (a)
- Determine all local maxima, minima, and saddle points. Are the
local extrema also global extrema?
- (b)
- Match the function h(x,y) in part (a) to the plot of its level
curves. Explain.
- 6.
- We want to compute the volumes of the objects below. Give the
integrand and the limits of integration in each case. (No reasons need be
given. Note that
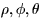 are spherical coordinates and that
are spherical coordinates and that
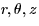 are cylindrical coordinates.)
are cylindrical coordinates.)
- (a)
- A wedge of a cantaloupe, cut from a perfect sphere.
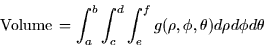
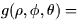



- (b)
- A spherical bead with a cylindrical hole cut through the center.
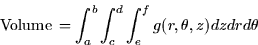
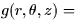



- 7.
- Consider the plane 2x + y - 5z = 7 and the line with parametric
equation
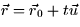 .
.
- (a)
- Give a value of
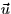 which makes the line perpendicular to the
plane.
which makes the line perpendicular to the
plane.
- (b)
- Give a value of
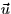 which makes the line parallel to the
plane.
which makes the line parallel to the
plane.
- (c)
- Give values for
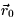 and
and 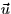 which make the line lie
in the plane.
which make the line lie
in the plane.
- 8.
- Let
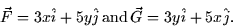
Let C1 be the circle with center (2,2) and raius 1, oriented
counterclockwise. Let C2 be the path consisting of the straight line
segment from (0,4) to (0,1), followed by the straight line segment from
(0,1) to (3,1). Find the following line integrals. Explain your
reasoning.
- (a)
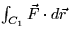
- (b)
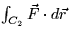
- (c)
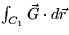
- (d)
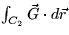
- 9.
- Consider the vector field
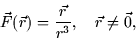
where  and
and 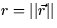 .
.
- (a)
- Show that div
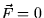 for
for 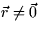 .
. - (b)
- Let S be the surface of a ball centereed at the origin. LEt
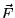 be the same vector field as in part (a). Do the Divergence
Theorem and your answer to part (a) imply that
be the same vector field as in part (a). Do the Divergence
Theorem and your answer to part (a) imply that 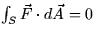 ? Explain why or why not.
? Explain why or why not.
- 10.
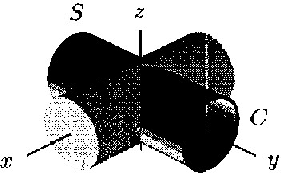
- Suppose W is the object consisting of two solid cylinders meeting
at right angles at the origin. One cylinder is centereed on the y-axis,
between y = -5 and y = 5 with radius 2 and the other is centered on the
x-axis between x = -5 and x = 5 with radius 2. Let S be the whole
surface of W except for the circular end of the cylinder centered at
(0,5,0). The boundary of S is a circle, C; the surface S is oriented
outward. Let
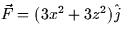 . You are also told that
. You are also told that
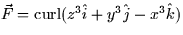 .
.
- (a)
- Suppose you want to calculate
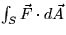 .Write down two other integrals which have the same value as
.Write down two other integrals which have the same value as 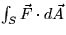 . Justify your answer.
. Justify your answer.
- (b)
- Find
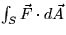 by whatever method is
easiest.
by whatever method is
easiest.
Vector Calculus
1/14/1998
 .
. and
and 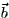 .
. 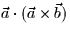 ?
Why?
?
Why?
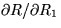 .
.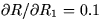 for some values of R1
and R2. What does this tell you, in terms of resistances?
for some values of R1
and R2. What does this tell you, in terms of resistances?
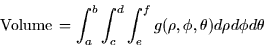
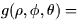



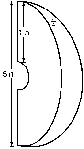
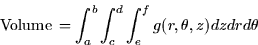
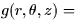



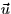 which makes the line perpendicular to the
plane.
which makes the line perpendicular to the
plane.
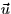 which makes the line parallel to the
plane.
which makes the line parallel to the
plane.
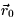 and
and 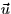 which make the line lie
in the plane.
which make the line lie
in the plane.
![]()
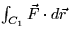
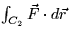
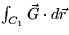
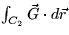
![]()
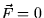 for
for 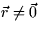 .
.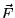 be the same vector field as in part (a). Do the Divergence
Theorem and your answer to part (a) imply that
be the same vector field as in part (a). Do the Divergence
Theorem and your answer to part (a) imply that 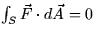 ? Explain why or why not.
? Explain why or why not.
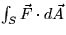 .Write down two other integrals which have the same value as
.Write down two other integrals which have the same value as 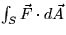 . Justify your answer.
. Justify your answer.
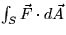 by whatever method is
easiest.
by whatever method is
easiest.