Part I: Short Questions
Answer each of the following short questions. Give a brief justification
for your answer.
| x | ||||
| -1 | 0 | 1 | ||
| 1.0 | 0.7 | 0.1 | -0.5 | |
| y | 1.2 | 4.8 | 4.2 | 3.6 |
| 1.4 | 8.9 | 8.3 | 7.7 |
Does the gradient vector of f at (0,1.2) point into a) the first quadrant, b) the second quadrant, c) the third quadrant, or d) the fourth quadrant. Justify your answer.




Part II: Longer Questions
PV = RT
for a certain fixed amount of a gas (called a mole of gas), where P is the pressure (in atmospheres), V is the volume (in cubic meters), T is the temperature (in degrees Kelvin) and R is a positive constant.- (a)
- Find
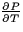 and
and 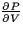 .
. - (b)
- A mole of a certain gas is at a temperature of 298 degrees Kelvin, a
pressure of 1 atmosphere and a volume of 0.0245 m3. Calculate
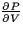 for this gas. Give the units of your
answer and explain what it means in practical terms.
for this gas. Give the units of your
answer and explain what it means in practical terms.
- (a)
- Using spherical coordinates, write a triple integral which represents this volume.
- (b)
- Evaluate the integral.
- (a)
- Give a value of
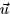 which makes the line perpendicular to the
plane.
which makes the line perpendicular to the
plane.
- (b)
- Give a value of
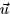 which makes the line parallel to the
plane.
which makes the line parallel to the
plane.
- (c)
- Give values for
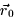 and
and 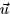 which make the line lie in
the plane.
which make the line lie in
the plane.
![]()
- (a)
- Find the flux of
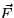 out of the sphere of radius 1 centered at
the origin.
out of the sphere of radius 1 centered at
the origin.
- (b)
- Show that div
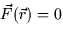 for all
for all 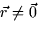 .
. - (c)
- Use parts (a) and (b), and the Divergence Theorem, to calculate the
flux of
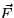 out of a cube of side 3 centered at the origin. [Note:
it is possible to answer this question without a long involved
calculation.]
out of a cube of side 3 centered at the origin. [Note:
it is possible to answer this question without a long involved
calculation.]
- (a)
- Calculate curl
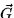 .
. - (b)
- Let C be a simple closed curve lying in the xy-plane. Use your
answer to part (a) and Stokes' theorem to show that
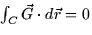 . To receive full credit you must state Stokes' Theorem
accurately and explain carefully how it applies.
. To receive full credit you must state Stokes' Theorem
accurately and explain carefully how it applies.