Section 11.4
#1. To find the contours, we set z equal to a constant, say c. Then we solve the resulting equation, c = x + y, for y to get: y = -x + c. Thus, the contours of f(x, y) = x + y are all straight lines which have a slope of 1 (the coefficient of x) and a y-intercept of c (the z value on that contour.) Thus, we get the contour diagram shown below.
#2. Setting z = c for z = x y, produces the contours y = (c/x). These contours are all hyperbolas, except for x = 0 or y = 0, which form the z = 0 contour. Note that the contour for z = 0 is actually two lines which cross. This does not violate the law that contours of different z values can never cross, since on both lines we find z = 0. This contour diagram is shown below.
#3. Setting c = x2 + y2, we see that c = 0 is
a point (the origin) and for c > 0, the contours are circles, centered
at the origin with a radius ![]() .
Note that the contours are all concentric, but as you go farther from the
origin, the contours for equally spaced z values get closer together. There
are no contours for c < 0, since x2 + y2 > 0.
.
Note that the contours are all concentric, but as you go farther from the
origin, the contours for equally spaced z values get closer together. There
are no contours for c < 0, since x2 + y2 > 0.
#4. This function is similar to #1, except for the factor of 3. These contours are similar, except that the y-intercepts of the lines are at (c/3). Thus, they are more closely spaced than the contours in #1, indicating that the plane (this is a linear function) is steeper.
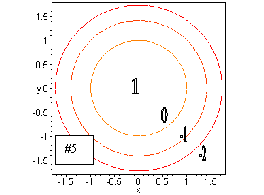
#5. This function is similar to the function in #3. In fact, it is the
function from #3 flipped upside down along the z axis (the negative sign
in front of x2 + y2,) and shifted up by 1. The contours
here are also circles centered at the origin, but these have a radius ![]() .
In order for this radius to make sense, we must choose contours with c
values which make 1-c > 0. In other words, c < 1. Again, these contours
are getting closer together as we move out from the origin, but in this
case, the z values on the contours is decreasing.
.
In order for this radius to make sense, we must choose contours with c
values which make 1-c > 0. In other words, c < 1. Again, these contours
are getting closer together as we move out from the origin, but in this
case, the z values on the contours is decreasing.
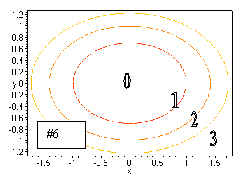
#6. The equation x2 + 2y2 = c is the equation
of an ellipse with x intercepts at (![]() ,0)
and (-
,0)
and (-![]() ,0) and y intercepts at
(0,
,0) and y intercepts at
(0, ![]() ) and (0,-
) and (0,- ![]() ).
).
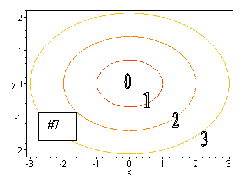
#7. This function is simply the square root of the previous function.
The contours here will also be ellipses, but the x intercepts are at (c,0)
and (-c,0) and the y intercepts are at (0,c/![]() )
and (0, -c/
)
and (0, -c/![]() ).
).
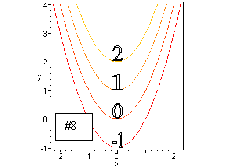
#8. The contours for f(x, y) = y x2 are parabolas: y = x2 + c. Thus, the vertex of the parabolas is at (0,c) and the parabola opens upward (coefficient of x2 is positive.)
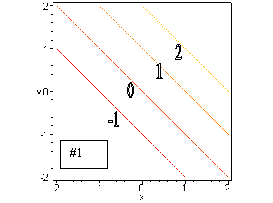
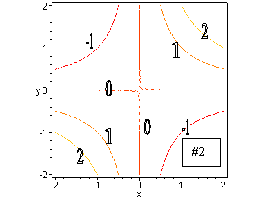
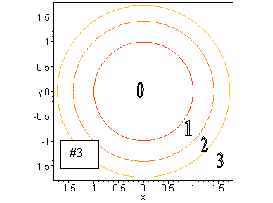
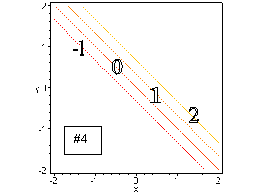
#11. (a) Since the contours near point A are closer together, we can
walk a shorter distance (xy distance) and cover a larger change of z than
we can at point B. In fact, at point A it looks as if a walk of about 1
cm (on graph scale) will take us from z = 100 to z = 300. At B, a walk
of the same distance will increase z from 100 to about 200.
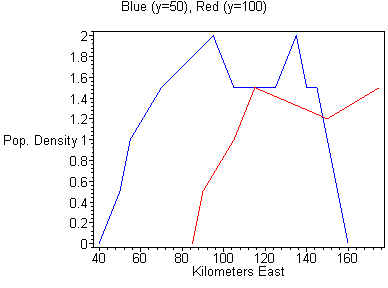
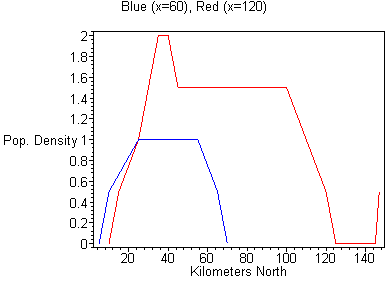
#16. In order to draw cross-sections along a north-south line, pick two values of x (like 60 and 120.) Now look along the line x = 60 and determine the coordinates of the points along the line (note that some coordinates are approximated): (60,5,0), (60,10,0.5), (60,25,1), (60,55,1), (60,65,0.5), (60,70,0) and similarly for x = 120. Then plot these points on a set of y-z axes. You should have two lines on the same axes, one with x = 60 and one with x = 120. Since a contour diagram is an overhead view of the surface which represents a function of two variables, this "slicing" in x will produce several side views of the surface, each at different x values. Fixing y (say at 50 and 100) can be done to produce a similar set of cross-sections on a set of x-z axes. These graphs are shown below.
#23. Since (a) and (d) have circular symmetry, as does graph (e) we
know that these should match in some way with (ii), (iii), and (iv). Since
graph (a) is mostly negative, we would chose contour diagram (iii). The
contours of (d) should be equally spaced and increasing so this goes with
(ii). Thus, graph (e) matches (iv). The contours of (b) should be lines
parallel to the x axis so this goes with (i) leaving (c) and (v).
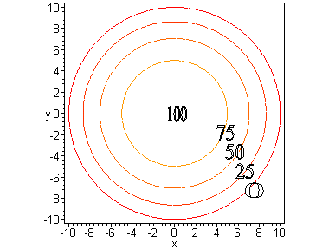 #25. Note that the isothermal curves (which are contours: the
prefix iso means "same" so an isobar is a line of constant pressure,
measured in bars) are circles since the function can be written as
#25. Note that the isothermal curves (which are contours: the
prefix iso means "same" so an isobar is a line of constant pressure,
measured in bars) are circles since the function can be written as ![]() which clearly exhibits
circular symmetry. The circles have a radius of
which clearly exhibits
circular symmetry. The circles have a radius of ![]() where c is the value of the function T(x,y) on the contour. Thus the maximum
value of T is 100, which occurs on a circle of radius 0. The contour with
T = 0 has radius 10. Note that the circles get closer together as the point
(x, y) moves farther from the origin. If a heat-seeking bug (lets call
it Roger) is dropped at some point (x, y) in the plane, then Roger will
move toward the origin, since the origin is the hottest point. Note that
this path (from the point (x, y) to the point (0, 0)) is always perpendicular
to the level curve (contour, isotherm) through the point (x, y).
where c is the value of the function T(x,y) on the contour. Thus the maximum
value of T is 100, which occurs on a circle of radius 0. The contour with
T = 0 has radius 10. Note that the circles get closer together as the point
(x, y) moves farther from the origin. If a heat-seeking bug (lets call
it Roger) is dropped at some point (x, y) in the plane, then Roger will
move toward the origin, since the origin is the hottest point. Note that
this path (from the point (x, y) to the point (0, 0)) is always perpendicular
to the level curve (contour, isotherm) through the point (x, y).
#26. The following answers are reasonable temperatures for the contours, starting with the contour closest to the window and moving outward into the room. All temperatures are given in degrees Fahrenheit.
(a) 15, 20, 25 (b) 30, 40, 50 (c) 95, 90, 85 (d) 80, 70, 60
#30.
#5. The equation for the xz-plane is y=0. Plugging this into the form of a linear function of two variables (z = c + mx + ny) we get z = c + mx. Matching this up with z = 3x + 4, we see that c = 4 and m = 3. Likewise, the yz-plane is x=0, so we plug this in and match up to the other equation, finding that n = 1. Thus, the equation of the linear function is simply z = 4 + 3x + y.
#6. Starting with the second piece of information, we see that if the point (0, 0, 5) is on the plane given by z = c + mx + ny, then c = 5. We can utilize the other piece of information by plugging the equation for the xy-plane (z = 0) into the linear equation and then solving for y to match up with the line y = 3x+4. We get that y = (-m/n)x (4/n) = 3x + 4. Thus, -5/n = 4, leaving n = -5/4. Since we know that m/n = 3, this tells us that m = 15/4. The equation of the plane is then z = 5 + (15/4)x (5/4)y.
#11. Using the points (2,0,3) and (2,1,5) we see that the slope in the y direction for this plane is n = (5-3)/(1-0) = 2. Thus, the point with x = 0 and y = 0 has z = 1-2 = -1. We can also get this from the points (0,1,1) and (2,1,5), finding the slope in the x direction to be m = (5-1)/(2-0) = 2 so that for a change of -2 in x (from 2 to 0) leads to a change in z of 4 so that z = -1 at x = 0, y = 0.
#12. Using (3,0,3) and (3,1,5) we see that n = (5-3)/(1-0) = 2 so that x = 3, y = -1, yields z= 1. We can now find m = (1-4)/(3-2) = -3 and get that the remaining points in the table are (2,0,6) and (2,1,8).
#14. This problem is similar to the last two, except that we can choose our own points. To get the slope in the x direction, pick two points with the same y value: (4,6,-105) and (16,6,-45) for instance. Then m = (-45 - -105)/(16-4) = 60/12 = 5. Picking two points with the same x value, like (4,0,-75) and (4,6,-105), gives us n = (-105- -75)/(6-0) = -5. Thus the equation of the plane is something like z = c + 5x 5y. To find c choose one point and plug it in. Taking (4,0,-75) we see that 75 = c + 5(4) 5(0) = c + 20 so that we know c = -95 and the equation is z = -95 + 5x 5y.
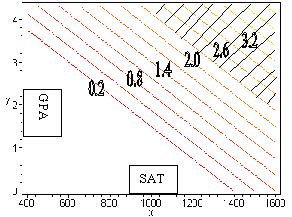 #19. This question uses the linear function f(x,y) = 0.003x +0.8y
4.
#19. This question uses the linear function f(x,y) = 0.003x +0.8y
4.
Section 11.6
#3. Each of these functions is a function of three variables (x, y, z) which is represented by a series of nested cylinders for its level surfaces. The variable which is missing in each function tells us which of the coordinate axes is lined up with the axis of the cylinder. Since x is missing in (a), this must match graph (i) and (b) must match graph (ii).
#6. The first thing to note about this function of (x, y, t) is that it varies between 19 and 21 (since it is simply a sine function shifted up 20 units.) For a fixed value of t, we can draw a cross section of the hyper-surface which represents this function. We could also draw a contour diagram of z = f(x, y, T) where T is a fixed number. The contours will all be lines with a slope of 1: y = -x + T + sin-1(w-20). There are an infinite number of lines for each value of w between 19 and 21 since the inverse sine function has infinite solutions (ex. The inverse sine of 0 is any integer multiple of pi.) As T increases, the y intercept of the contours will shift up, but the slope will remain constant. This represents a series of waves flowing across the surface of the water, as shown in the brief animation below.
#11. This problem is similar to Section 11., #14, except that there is one more variable to deal with. Using the contour diagram for z = 3, we read off the four points f(0,1,3) = 2, f(0,-1,3) = 8, f(2,0,3) = 2, f(-2,0,3) = 8. We can then compute the slopes in the x and y direction: a = (8 2)/(-2-2) = -6/4 = -3/2 and b = (2-8)/(1- -1) = -6/2 = -3. To get the slope in the z direction (given by c) we would need two points with the same x and y values, but different z and f values. Looking at the two contour diagrams, there are no such points given. Instead, we can find c and d simultaneously by finding two equations and solving for these two unknowns. We know that f(0,1,3) = 2 and f(0,0,4) = 8, so if we plug this into the linear function (and use the constants a and b which we have) we get the two equations 5 = 3c + d and 8 = 4c + d. Subtracting the first equation from the second yields c = 3. Substituting this into the first equation, we find that d = -4, so that the equation of the linear function is f(x, y, z) = (-3/2)x 3y + 3z 4.
Section 12.1
#1. We can match the vectors up graphically. Boldface, uppercase letters denote a vector, rather than a name with an arrow over it. P = 2W, Q = -U, R = U + W, S = P + Q = 2W U, T = R 2W = U W.
#2. See below.
#8. 2A + 7B 5Z = 2(2,1,0) + 7(-3,5,4) 5(1,-3,-1) = (4,2,0) + (-21,35,28) (5,-15,-5) = (-22,52,33).
#9. (4i + 2j) (3i j) = (4-3)i + (2+1)j = i + 3j.
#11. 4(1,-2,0) 0.5(1,0,-1) = (-4,8,0) (0.5,0,-0.5) = (-4-0.5, 8-0, 0+0.5) = (4.5,8,0.5)
#16. ||B|| = ||(7.2, -1.5, 2.1)|| = ![]() .
.
#24. The vector QP goes from (4,6) to (1,2) so it moves (1-4)=-3 to the right and (2-6)= - 4 up. Thus the vector QP = -3i 4j.
#25. We can resolve these vectors into components by two methods: either looking at how far the vector points in each direction, or by writing down the coordinates of the endpoints for each vector and then subtracting (final initial.) Well use the first method for all of these except D. A = (0,0,3), B = (0,0,3), C = (0,0,3), E = (0,1,0), F = (-2,0,0) and D = (1,0,3) (0,0,0) = (1,0,3).
#28. To find a vector with the same direction as U = (1,-1,2)
but with a length 2 we proceed in two steps. First, we turn U into
a unit vector by dividing the vector by its magnitude: U/||U||
= (1,-1,2)/![]() = (1/
= (1/![]() ,
-1/
,
-1/![]() , 2/
, 2/![]() ).
Now that the vector has length 1 (and same direction since we have only
multiplied by a positive scalar) we simply make it 2 units long by multiplying
it by 2. The new vector is then given in components by (2/
).
Now that the vector has length 1 (and same direction since we have only
multiplied by a positive scalar) we simply make it 2 units long by multiplying
it by 2. The new vector is then given in components by (2/![]() ,
-2/
,
-2/![]() , 4/
, 4/![]() ).
You can compute the magnitude of this vector to verify that it has length
2.
).
You can compute the magnitude of this vector to verify that it has length
2.
#30. In order for two vectors to be parallel, they must be scalar multiples of each other. For the vectors listed, we find that Q = 4V and U = -2W. Thus, only Q and V are parallel. (The other two vectors, U and W) are anti-parallel, since the scalar multiple is negative, indicating that the two vectors face opposite directions.)
Drawings for 12.1 #2.
