Homework Four
Section 13.1 .
#3. (a) In financial terms, the fact that f(92000,14,30) = 1090.08 tells me that a loan of $92,000 dollars (to buy a house) at a rate of 14% interest for 30 years will result in a monthly mortgage payment of $1090.08. This is more than I, as a graduate student can afford, so I would choose not to buy the house. (b) The number 72.82 shows that if the interest rate on the previously discussed loan were to go from 14% to 15%, my monthly mortgage payment would increase $72.82. (c) One would expect the sign of ![]() to be positive. The logic here is that if I borrow more money (increase A) while keeping the same number of payments at the same interest rate, the amount of each payment should go up. (d) The sign of
to be positive. The logic here is that if I borrow more money (increase A) while keeping the same number of payments at the same interest rate, the amount of each payment should go up. (d) The sign of ![]() should be negative, since the monthly payment will be less if we spread the same loan amount (A) over a longer period of time (N) at the same interest rate (r).
should be negative, since the monthly payment will be less if we spread the same loan amount (A) over a longer period of time (N) at the same interest rate (r).
#6. (a) One would expect the units of ![]() to be in units of concentration divided by units of distance. This would be something like (kg/mm^3)/(mm). Practically, this tells how the concentration of the drug (measured by c) changes with distance (x) from the point of the injection. The sign of this derivative should be positive as the drug reaches new areas in the blood. (b) The sign of
to be in units of concentration divided by units of distance. This would be something like (kg/mm^3)/(mm). Practically, this tells how the concentration of the drug (measured by c) changes with distance (x) from the point of the injection. The sign of this derivative should be positive as the drug reaches new areas in the blood. (b) The sign of ![]() will be negative, since the concentration will decrease in time, as the drug slowly spreads throughout the system. Its units will be in concentration per unit time, something like (kg/mm^3)/second. Practically, this derivative shows the rate of change in the concentration of the drug at a point x at time t as time increases.
will be negative, since the concentration will decrease in time, as the drug slowly spreads throughout the system. Its units will be in concentration per unit time, something like (kg/mm^3)/second. Practically, this derivative shows the rate of change in the concentration of the drug at a point x at time t as time increases.
#8. (a) At point A on the surface, if one walks in the +x direction, one will be walking uphill, so the sign of ![]() at A is positive. (b) On the other hand, as one walks in the direction of increasing y, one is walking downhill. Thus,
at A is positive. (b) On the other hand, as one walks in the direction of increasing y, one is walking downhill. Thus, ![]() at A is negative. (c) As one walks along a straight line in the xy plane from A to B, one sees that the derivative in the y direction is always negative, while the derivative in the x direction starts off positive and then decreases in magnitude till the point P reaches x = 0 where the x derivative is zero. From here on to point B, the sign of
at A is negative. (c) As one walks along a straight line in the xy plane from A to B, one sees that the derivative in the y direction is always negative, while the derivative in the x direction starts off positive and then decreases in magnitude till the point P reaches x = 0 where the x derivative is zero. From here on to point B, the sign of ![]() becomes negative, since one is walking downhill.
becomes negative, since one is walking downhill.
#10. One can estimate the value of ![]() by approximating the difference quotient. In other words, one takes the value of the function at the point nearest (10,25) in the direction of increasing W. This would be the point (15,25). This is a change in W of (15-10) = 5. The function changes from f(10,25) = 10 to f(15,25) = 2. Thus the derivative is approximately
by approximating the difference quotient. In other words, one takes the value of the function at the point nearest (10,25) in the direction of increasing W. This would be the point (15,25). This is a change in W of (15-10) = 5. The function changes from f(10,25) = 10 to f(15,25) = 2. Thus the derivative is approximately ![]() . This value means that if the temperature is actually 25 Fahrenheit and the wind speed is 10 mph, then an increase in the wind speed of 1 mph would decrease the apparent temperature of the air by 1.4 degrees.
. This value means that if the temperature is actually 25 Fahrenheit and the wind speed is 10 mph, then an increase in the wind speed of 1 mph would decrease the apparent temperature of the air by 1.4 degrees.
#11. To estimate ![]() we look at the function at the nearest point in the direction of increasing T. This would be the point f(5,25) = 21. The difference quotient is then given simply by
we look at the function at the nearest point in the direction of increasing T. This would be the point f(5,25) = 21. The difference quotient is then given simply by ![]() . This tells us that with a wind speed of 5 mph and an actual temperature of 20 degrees Fahrenheit, an increase in the outdoor temperature of one degrees will result in an increase in the apparent temperature of 1 degree Fahrenheit.
. This tells us that with a wind speed of 5 mph and an actual temperature of 20 degrees Fahrenheit, an increase in the outdoor temperature of one degrees will result in an increase in the apparent temperature of 1 degree Fahrenheit.
#12. If the apparent temperature is dropping by 2.6 degrees for each 1 mph increase in wind speed when the temperature is actually 20 and the wind speed is between 5 and 10, this tells us that ![]() = -2.6.
= -2.6.
#13. Just as in the previous problems, one can approximate these partial derivatives as difference quotients. Here, we read the values of the function from the contour diagram, rather than a table. (a) ![]() dollars per percent increase in interest. Note that we chose the point P(12,4000) since at this point we can approximate the function as being half-way between the contour for P = 100 and P = 80. In order the estimate the derivative in the L direction we act similarly:
dollars per percent increase in interest. Note that we chose the point P(12,4000) since at this point we can approximate the function as being half-way between the contour for P = 100 and P = 80. In order the estimate the derivative in the L direction we act similarly:
![]() dollars per dollar increase in the loan amount. (b)
dollars per dollar increase in the loan amount. (b) ![]() dollars per percent increase in r.
dollars per percent increase in r. ![]() dollars per dollar increase in loan amount. (c) Using the points P(8,7000) = 140 and P(13,7000) = 160 one can estimate that
dollars per dollar increase in loan amount. (c) Using the points P(8,7000) = 140 and P(13,7000) = 160 one can estimate that ![]() with a backward difference quotient. One can also use P(13,8000) = 180 and P(13,7000) = 160 to get
with a backward difference quotient. One can also use P(13,8000) = 180 and P(13,7000) = 160 to get ![]() . Keep in mind that all of these partial derivatives are estimates not actual values, since we are approximating the difference quotients with finite (rather than limiting) values of h.
. Keep in mind that all of these partial derivatives are estimates not actual values, since we are approximating the difference quotients with finite (rather than limiting) values of h.
Section 13.2 ..
#2. For the function f(u,v) = u(u^2+v^2)^(1/2):
#8.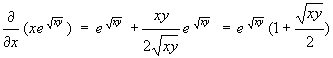 .
.
#9. ![]()
#15. 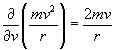
#21. 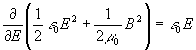
#29. ![]()
#36. To show that the given function Q satisfies the given partial differential equation, we simply take the appropriate derivatives and plug them into the equation.
![]() and
and ![]() . Plugging this into the equation, we see that
. Plugging this into the equation, we see that ![]() and that
and that ![]() so that the sum is definitely Q.
so that the sum is definitely Q.
Review of Derivatives
| (1) |
| = | 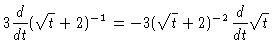 |
||
| = | 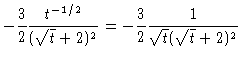 |
(2) |
| (3) |
| (4) |
| = |  |
||
| = | 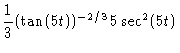 |
(5) |
| = | 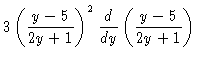 |
||
| = | 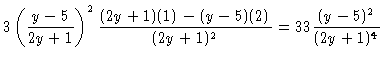 |
(6) |
| = | 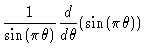 |
||
| = |  |
(7) |
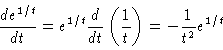 |
(8) |
| (9) |
| z | = | ||
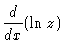 |
= | 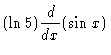 |
|
| = | 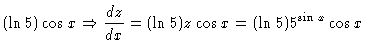 |
(10) |
| (11) |
| f(t) | = | 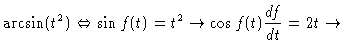 |
|
| = | 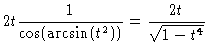 |
(12) |
| (13) |
| = | 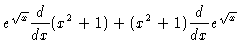 |
||
| = | ![$\displaystyle 2x e^{\sqrt{x}} + (x^2+1) e^{\sqrt{x}} \frac{d}{dx} \sqrt{x} =
e^{\sqrt{x}} \left[ 2x + (x^2 + 1)\frac{1}{2} x^{-1/2} \right]$](img32.gif) |
(14) |
| (15) |
| (16) |
| (17) |
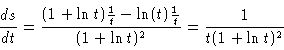 |
(18) |
| (19) |
| (20) |
| (21) |