Homework Five
Section 13.3
#1. The equation for the tangent plane to z = f(x, y) at the point (1,0,9) is z = f(1,0) + (x-1) fx(1,0) +
y fy(1,0). For the function given in this problem, the partial derivatives can be taken and we find that
z = 3 + 3(x-1) + y.
#4. (a) One immediately knows that the students answer is wrong since the answer is not a linear function of x and y. (b) The student forgot to evaluate the partial derivatives of the function at the point (2,3). (c) If the student had plugged the point in correctly, the answer would have been z = 12(x-2) 6(y-3) 1.
#10. The graph shown is a sectioning of the function ic = f(ib, vc). In order to compute a linear approximation to the function, one needs to evaluate the partial derivatives of the function. This involves using the difference quotients, since we do not have an algebraic representation for f. The linear approximation, L(i, v) = f(-300,-8) + (i + 300) fi(-300,-8) + (v + 8) fv(-300,-8). From the sectioning, one can estimate the partial derivatives as
![]()
![]()
so that we have the linear approximation as L(i, v) = - 31 + 0.09(i+300) + 0.5(v+8).
#11. Using the formula for the differential on page 114, we find
![]() .
.
#17. Using the formula on page 114 and evaluating the partial derivatives at the point (100,1) the differential becomes dP = 0.00798 dL + 2.3954 dK.
#21. (a) If the volume is held constant (so that dV = 0) and the temperature is increased slightly (so that dT > 0), one sees that the energy would increase, since dU = 27.32 dT > 0. (b) If the volume increases slightly and the temperature is held constant, the energy also increases. (c) If the gas is compressed by 100 cc (ie. dV = -0.0001 cubic meters) and the temperature is increased by 2K, we find a change in the energy of dU = 840(-0.0001) + 27.32(2) = 54.56.
#22. (a) Since density is mass divided by volume, we have ![]() since m is held constant ("a fixed quantity of a liquid".) Replacing dV by the formula given in the problem, one finds immediately that
since m is held constant ("a fixed quantity of a liquid".) Replacing dV by the formula given in the problem, one finds immediately that ![]() (b) Reading points from the graph and estimating difference quotients, we see that, at T = 20, d(rho) = 992 998 = -6 when dT = 40 20 = 20. Thus, at T = 20, the formula above gives us that (beta) = -(-6)/(998*20) = 0.0003. When T = 80, we find d(rho) = 958 970 = -12 for dT = 100-80=20. Thus, (beta) = -(-12)/(970*20) = 0.0006.
(b) Reading points from the graph and estimating difference quotients, we see that, at T = 20, d(rho) = 992 998 = -6 when dT = 40 20 = 20. Thus, at T = 20, the formula above gives us that (beta) = -(-6)/(998*20) = 0.0003. When T = 80, we find d(rho) = 958 970 = -12 for dT = 100-80=20. Thus, (beta) = -(-12)/(970*20) = 0.0006.
Section 13.4
#1. (a) The rate of change of f as you leave (1,4) going in the direction of the point (3,5) is the same as the directional derivative of f at the point (1,4) in the direction of the unit vector (2i + j)/sqrt(5). Thus,
![]() . (b) As you approach the point (3,5), the directional derivative is different since the partial derivatives are different at (3,5) and (1,4). Here, one finds
. (b) As you approach the point (3,5), the directional derivative is different since the partial derivatives are different at (3,5) and (1,4). Here, one finds ![]() .
.
#2. 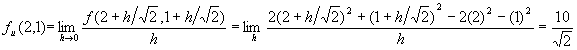
#5. At (3,1) the contours suggest that ![]() , this implies that the desired directional derivative is
, this implies that the desired directional derivative is ![]() . One can also estimate this by trying to locate the point that the vector u would take (3,1) to. However, this would be less accurate, since there would be more guess work required.
. One can also estimate this by trying to locate the point that the vector u would take (3,1) to. However, this would be less accurate, since there would be more guess work required.
#6. This problem is similar to #5. However, the vector u is different in this case, so the directional derivative is has the opposite sign as the answer in problem #5.
#9. (a) The given vector points toward the +x axis and toward the y axis. The surface slopes downhill in this direction, so the directional derivative is negative. (b) This vector points toward the +x and +y axes. In this direction, the surface slopes downhill, so again, the directional derivative is negative.
#13. ![]() #14.
#14. ![]()
#19. ![]() #20.
#20. ![]()
#30. The vector u is given in components by cos(5pi/4)i + sin(5pi/4)j. The gradient of this function is grad(z) = 2xyi + (x^2)j. The directional derivative is simply the dot product of these two, with the partial derivatives (in the gradient) evaluated at (1,2). The answer is 5/sqrt(2).
#32. To solve this problem, set up a system of two equations for the unknowns. In this case the unknowns are the partial derivatives. They enter the equations through the directional derivative by a dot product. For details, ask your instructor.
#34. (a) Since the function has circular symmetry, the level curves must be circles. They are centered at the origin. For equally spaced values of T, the radius of the circles spreads out quickly as T decreases from 100 at the center (0,0). (b) It is hottest in the center. The largest value of the temperature will occur when the denominator is as small as possible. The smallest the denominator gets is 1, which occurs at the origin. Here, T(0,0) = 100. (c) To answer this, compute the gradient at this point. The direction of greatest increase will be the direction of the gradient and the magnitude of the gradient will give the rate of increase in this direction. (d) The direction of greatest decrease in temperature is the direction opposite to the gradient. (e) Find a vector that is perpendicular to the gradient at (3,2). This vector will be in the same direction as the contour through (3,2) (Why?) When dotted with the gradient, the result is zero. Use this fact to find the vector. You may need to introduce additional equations (like the length of the vector.)
#36. (a) This is simply the partial derivative of f in the x direction. It is negative. (b) This is the partial derivative in the y direction at P. It is positive. (c) Positive. (d) Negative.
#37. The contours are closer together at P than Q, so the magnitude of the gradient is larger at P.
Section 13.5
#2. (a) ![]()
#5. To find a normal vector to the plane, form the gradient of the three variable function ![]() which is simply
which is simply ![]() . The tangent plane to this surface at (1,-1,-1) is simply
. The tangent plane to this surface at (1,-1,-1) is simply
-1(x-1) 3(y+1) 7(z+1) = 0.
#9. The contours are simply sine curves in the x direction. The y intercept of the curves is determined by the z value on the contour. The contour of this function that passes through (pi/2, 1, 0) has z = 0. To either side (right or left) as the bug walks, the contours have higher z values, so the bug must be in a valley. Remember, for part (c) the gradient is always perpendicular to the contours in the direction of increasing f.
#10. (a) You should move in the direction of the gradient at (-1,1,1) in order to increase the concentration of salt (the value of F(x,y,z)) the fastest. This would be in the direction of the vector (-4,4,2). (b) The rate of change of the concentration in this direction is the magnitude of the gradient, which is 6. This is measured in units of concentration per unit distance traveled. If we move in this direction at a rate of 4 units of distance per second, then the rate of change in the salt concentration is (6)(4) = 24 units of concentration per second.
#11. (a) To find a normal vector to the surface F = 0, compute the gradient of F. This is the vector ![]() . This vector is parallel to the xy plane when the k component is zero and the other two components are non-zero. This occurs along the plane y = 0. For F = 0, this implies that x = 0 also. Thus, only points (0,0,z) satisfy this condition. This describes the z axis. (b) The tangent plane can be found by evaluating the gradient at the specified points to get a normal vector and then using the formulas from 12.3. At (0,0,1) the tangent plane is y = 0. At (1,1,1) the tangent plane is 2(x-1) (y-1) 2(z 1) = 0. (c) To find these unit vectors in the direction of maximum increase in the function at the points (0,0,1) and (1,1,1) make a unit vector out of the gradient at these points. The results are the vector (0,1,0) and (2/3, -1/3, -2/3).
. This vector is parallel to the xy plane when the k component is zero and the other two components are non-zero. This occurs along the plane y = 0. For F = 0, this implies that x = 0 also. Thus, only points (0,0,z) satisfy this condition. This describes the z axis. (b) The tangent plane can be found by evaluating the gradient at the specified points to get a normal vector and then using the formulas from 12.3. At (0,0,1) the tangent plane is y = 0. At (1,1,1) the tangent plane is 2(x-1) (y-1) 2(z 1) = 0. (c) To find these unit vectors in the direction of maximum increase in the function at the points (0,0,1) and (1,1,1) make a unit vector out of the gradient at these points. The results are the vector (0,1,0) and (2/3, -1/3, -2/3).