[2] #1#2
Homework Six
Please be aware that there are several typos, due to
the conversion program which put the solutions onto the web. I am sorry,
but at the moment, I cannot repair these.
Section 13.6
# 1. Using the chain rulle
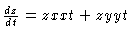 .
The appropriate partial derivatives are:
.
The appropriate partial derivatives are:
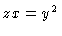 ,
,
 ,
,
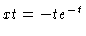 ,
and
,
and
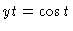 .
Thus,
.
Thus,
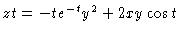 .
To get the final answer, insert the functions x(t) and y(t) to get
.
To get the final answer, insert the functions x(t) and y(t) to get
![$\Pd{z}{t} = e^{-t} \left[ -t\sin^2 t + 2 \sin t \cos t \right]$](img7.gif) .
#2. The chain rule gives the same general formula for
.
#2. The chain rule gives the same general formula for 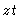 as
in number 1. The appropriate derivatives are:
as
in number 1. The appropriate derivatives are:
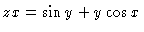 ,
,
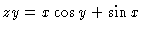 ,
,
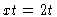 ,
and
,
and
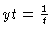 .
Thus,
.
Thus,
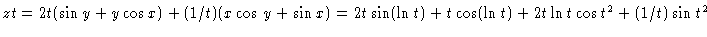 .
#7. The chain rule for
z = f(x,y) with x=x(u,v) and y=y(u,v)
gives us
.
#7. The chain rule for
z = f(x,y) with x=x(u,v) and y=y(u,v)
gives us
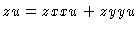 and
and
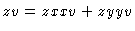 .
The
appropriate derivatives are
.
The
appropriate derivatives are
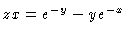 ,
,
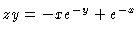 ,
,
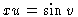 ,
,
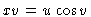 ,
,
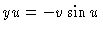 ,
and
,
and
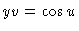 .
Thus, we find that
the two partial derivatives of z are:
.
Thus, we find that
the two partial derivatives of z are:
#8. The appropriate derivatives are:
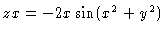 ,
,
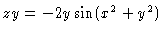 ,
,
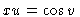 ,
,
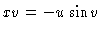 ,
,
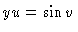 ,
and
,
and
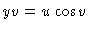 .
Using the chain rule as written in problem 7, we find
.
Using the chain rule as written in problem 7, we find
#19. An example of a homogeneous function is the function
f(x,y) =
x2 + y2 since
f(tx,ty) = (tx)2 + (ty)2 = t2 x2 + t2 y2 = t2
(x2 + y2) = t2 f(x,y). Thus, for this function, p = 2. Other
functions would potentially have different values of p. To simplify
matters, let u = tx and v = ty. Then, for
g(t) = f(tx, ty) =
f(u,v) we have that
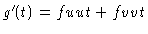 .
Now, ut = x and vt = y. Also, at t = 1 we have
that u=x and v=y so that
g'(1) = xfx + yfy. This is the right
hand side of the statement to be proved. However, since f(x,y) is a
homogeneous function, we also have that
g(t) = tp f(x,y). Taking
derivatives, we find that
g'(t) = p tp-1 f(x,y) so that
g'(1) =
p f(x,y). Since these two ways of computing g'(1) must be equal,
the statement
.
Now, ut = x and vt = y. Also, at t = 1 we have
that u=x and v=y so that
g'(1) = xfx + yfy. This is the right
hand side of the statement to be proved. However, since f(x,y) is a
homogeneous function, we also have that
g(t) = tp f(x,y). Taking
derivatives, we find that
g'(t) = p tp-1 f(x,y) so that
g'(1) =
p f(x,y). Since these two ways of computing g'(1) must be equal,
the statement
x fx(x,y) + y fy(x,y) = p f(x,y)
is proved.
Section 13.7
#3. For the function
f(x,y) = xey:
#8. For the function
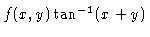 we use the fact that
the derivative of the arctangent (the inverse tangent) is given by
we use the fact that
the derivative of the arctangent (the inverse tangent) is given by
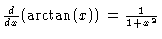 and the chain rule
to find that
and the chain rule
to find that
One quickly find that all of the second partial derivatives are
equal. This is to be expected, since the oringinal function f
depends on both x and y in the same way.
#9. If
z = f(x) + y g(x) then we see that
zy = g(x) and
zyy
= 0 since the function depends only linearly on y. Thus, the cross
sections of this function for fixed values of x will all be lines in
a plane parallel to the yz plane.
#10. If
zxy = 4y then (a)
zyx = 4y since the mixed partial
derivatives of a continuous function are the same, (b)
zxyx = 0
since
zxyx = (4y)x = 0, and (c)
zxyy = 4 since
zxyy =
(4y)y = 4.
For problems #11 through #19, here are the answers as a list. For
each problem, the signs of the derivatives are listed in the order
fx, fy, fxx, f, and fxy.
#11.
+, 0, +, 0, 0
#12.
+, 0, -, 0, 0
#13.
-, 0, -, 0, 0
#14.
-, 0, +, 0, 0
#15.
0, -, 0, -, 0
#16.
0, +, 0, -, 0
#17.
-, -, 0, 0, 0
#18.
+, -, -, -, +
#19.
-, +, +, +, -
Review of Integration
For each of the following problems, the name of the method used to
most easily obtain the antiderivative is given first. If you want
practice, try just looking at these hints and not the final answer.
If you're stuck, or sure you've got it right, check the answer.
#1. [U substitution] Let
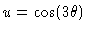 so that
so that
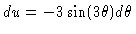 or
or
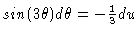 then the integral becomes
then the integral becomes
#2. [U substitution] Let
u = 43t. Then (using the correct
derivative law, which is NOT the power law)
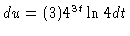 or
or
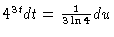 .
The integral is then
.
The integral is then
#3. [Power rule-after simplification] Split the fraction up into
three terms
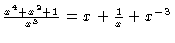 then
integrate with the normal power law to get
then
integrate with the normal power law to get
#4. [U substitution] Try letting
 so that
so that
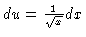 and then
and then
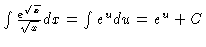 .
The final answer is then
.
The final answer is then
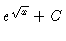 .
.
#5. [Trig Substitution-or memorization] Let
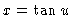 so that
so that
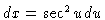 the integral then becomes
the integral then becomes
Now the trig identities tell us that
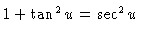 so
that the integral is really just
so
that the integral is really just
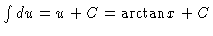 .
.
#6. [Exponential Rule-after simplification] Since
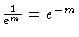 we can simply let u = -m so that du = -dm and the integral
is
we can simply let u = -m so that du = -dm and the integral
is
#7. [U substitution] Let
u = 4v + 7 then du = 4 dv and
#8. [Power Rule-after simplification] First multiply out the
polynomial so that you get
(1 + 3r2)2 = 1 + 6r2 + 9r4 and then
integrate to get
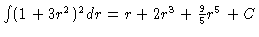 .
.
#9. [U substitution] Let
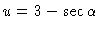 so that
so that
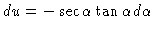 .
Then the integral becomes
.
Then the integral becomes
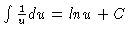 .
So that the final answer is
.
So that the final answer is
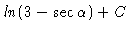 .
.
#10. [U substitution-after simplification] Use the properties of
logarithms to write
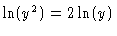 then let
then let 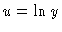 .
This makes
.
This makes
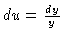 which is already present in the
integral. Thus, the integral is really
which is already present in the
integral. Thus, the integral is really
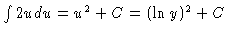 .
.
#11. [U substitution] Let u = w3 so that
du = 3w2 dw or
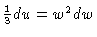 .
The integral is then
.
The integral is then
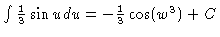 .
.
#12. [Simplification] Try writing the integrand as
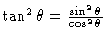 .
The numerator of this can be
rewritten as
.
The numerator of this can be
rewritten as
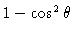 so that the integrand is really
so that the integrand is really
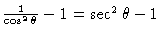 .
The integral is
then easily computed as
.
The integral is
then easily computed as
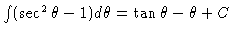 .
.
#13. [Rewrite the Integrand] Recall that
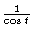 is just
is just
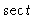 so the integrand is really
so the integrand is really 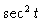 .
Recall also that
.
Recall also that
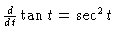 so the integral is just
so the integral is just
 .
.
#14. [U Substitution-with Simplification] The denominator of the
integrand can be factored to the form (x+3)2. Now a simple u
substitution of u = x + 3 results in the integration
Vector Calculus
1999-02-19
![]() so that
so that
![]() or
or
![]() then the integral becomes
then the integral becomes
![]() or
or
![]() .
The integral is then
.
The integral is then
![]() then
integrate with the normal power law to get
then
integrate with the normal power law to get
![]() so that
so that
![]() and then
and then
![]() .
The final answer is then
.
The final answer is then
![]() .
.
![]() so that
so that
![]() the integral then becomes
the integral then becomes
![]() we can simply let u = -m so that du = -dm and the integral
is
we can simply let u = -m so that du = -dm and the integral
is
![]() .
.
![]() so that
so that
![]() .
Then the integral becomes
.
Then the integral becomes
![]() .
So that the final answer is
.
So that the final answer is
![]() .
.
![]() then let
then let ![]() .
This makes
.
This makes
![]() which is already present in the
integral. Thus, the integral is really
which is already present in the
integral. Thus, the integral is really
![]() .
.
![]() .
The integral is then
.
The integral is then
![]() .
.
![]() .
The numerator of this can be
rewritten as
.
The numerator of this can be
rewritten as
![]() so that the integrand is really
so that the integrand is really
![]() .
The integral is
then easily computed as
.
The integral is
then easily computed as
![]() .
.
![]() is just
is just
![]() so the integrand is really
so the integrand is really ![]() .
Recall also that
.
Recall also that
![]() so the integral is just
so the integral is just
![]() .
.