Spring 1997
Due: Friday April 18, 1997
In this problem we derive the principle of conservation of Energy. The kinetic
energy of a particle moving with speed v is ![]() . For a
conservative vector field
. For a
conservative vector field ![]() with potential function f(x,y,z) (in the
physicist's sense) so that
with potential function f(x,y,z) (in the
physicist's sense) so that ![]() . The potential energy of a
particle at position
. The potential energy of a
particle at position ![]() is
is ![]() . The Conservation of Energy
Principle says that the expression
. The Conservation of Energy
Principle says that the expression
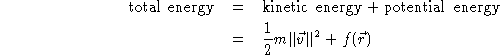
is constant for a particle moving in the field with position vector ![]() and velocity vector
and velocity vector ![]() . Let P and Q be two points in space and
let C be a path from P to Q parameterized by
. Let P and Q be two points in space and
let C be a path from P to Q parameterized by ![]() ,
, ![]() , where
, where ![]() and
and ![]() .
.
![]()