Math 223 Homework 7 Solutions

  1. If the particle is at position tex2html_wrap_inline193 then it has velocity tex2html_wrap_inline195 and an acceleration of tex2html_wrap_inline197 . In components, we can calculate

    equation30

    Now, using the chain rule, we see that

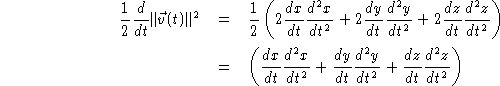
    eqnarray39

    Also, we see that tex2html_wrap_inline199 which shows that

    equation87

    An alternate way to see this calculation uses that fact that tex2html_wrap_inline201 . Now, we can calculate

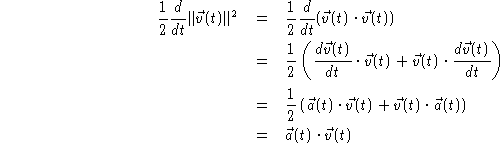
    eqnarray99

  2. Along the path C from P to Q the work done on a moving particle of mass m by a force tex2html_wrap_inline211 is

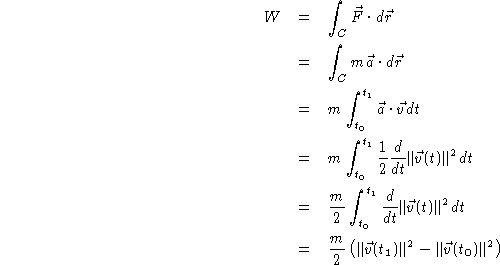
    eqnarray133

    This last step is due to the fundamental theorem of calculus for one variable integration (ie. tex2html_wrap_inline213 .) We see immediately that this expression is really the kinetic energy at Q minus the kinetic energy at P.

  3. Also, the work done on the particle by a force tex2html_wrap_inline219 is

    eqnarray167

    which is easily seen to be the potential energy at P minus the potential energy at Q.

  4. We now have two independent expressions for the work, so they must be equal. Equating the results of the previous parts, and then moving everything involving the point Q to one side, and everything involving P to the other, we see that

    equation175

    which is the expression for the Law of Conservation of Energy.