- (a)
- The component of
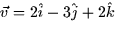 in the
direction of
in the
direction of  is
is 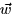 .
. - (b)
- Two contours of z = f(x,y) corresponding to different values of z can never cross.
- (c)
- The two planes 3z - 2x + y = 5 and -6z + 4x - 2y = 0 are parallel.
- (d)
- If f(x,y) is a linear function then f(3,4) - f(3,5) = f(4,4) - f(4,5).
- (a)
- Given the vectors in figure 1, draw the vector
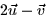 .
. - (b)
- Given that
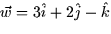 and
and 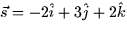 find:
find:
- i.
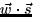
- ii.
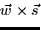
- iii.
- The angle between
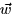 and
and 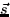 .
.
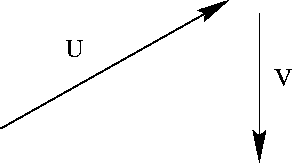
- (a)
- Find the equation of the plane z = f(x,y) corresponding to this diagram.
- (b)
- Find a unit normal vector to this plane.
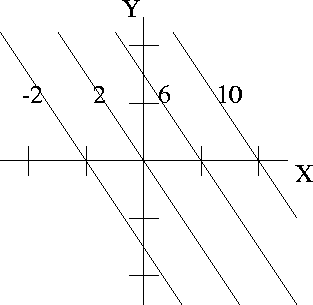
- (a)
- Draw a contour diagram and label the contours for z = 0.5, 1, 1.5.
- (b)
- What are the domain and range of f.
- (c)
- Is f(x,y) increasing or decreasing as a function of y at the point (1,0)?
- (a)
- Use the three cases above (1)-(3) to help determine the linear function that Fox uses to determine the score of a show.
- (b)
- If the show Married with Pets costs $1.5 million per epsiode and receives a Neilson rating of 60, what will happen to it?