- (a)
- The component of the vector
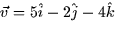 in the direction of the vector
in the direction of the vector 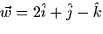 is
is
a. 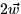
b. 2 c. 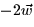
d. -2 - (b)
- The contours of the function
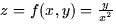 are
shaped like:
are
shaped like:
a. concentric circles b. parabolas c. hyperbolas d. parallel lines - (c)
- If f(x,y) is a linear function then the statement below is
f(4,5) - f(4,7) = f(2,2) - f(2,4)
a. always true b. always false c. true under certain conditions d. not enough information given - (d)
- Two planes z = ax+by+c and z=mx+ny+d are parallel if (more than
one answer may be correct):
a. their normal vectors are either 0 or 180 degrees apart b. their normal vectors are perpendicular c. the constants c and d are equal d. the quantities ax + by and mx + ny are equal for all x and y
- (a)
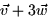
- (b)
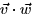
- (c)
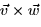
- (d)
- The angle,
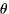 , between
, between 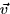 and
and 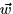
- (a)
- The following table represents values for a linear function of the
variables x and y. Find the equation for this linear function.
Y -1 1 X 2 14 12 3 18 - (b)
- Find a unit normal vector to the plane whose equation you found in above.
![]()
- (a)
- Draw the contours f(x,y) = c for c=0,1,2,3.
- (b)
- What is the domain (for both x and y) of the function?
- (c)
- Describe the contours f(x,y) = c as
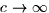 .
. - (d)
- Use the contour diagram to decide if f is an increasing, decreasing or constant function of the variable x at the point x=0, y=0.5.
- (a)
- If the Star Fury fires an energy weapon (speed =
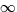 ) at the
Shadow vessel, what is the direction in which the pilot should fire?
This should be a unit vector.)
) at the
Shadow vessel, what is the direction in which the pilot should fire?
This should be a unit vector.)
- (b)
- Write the velocity of the Star Fury as a sum of two vectors, one along the direction of the Shadow vessel's velocity and one perpendicular to the Shadow vessel's velocity.
- (c)
- Find the equation of the plane containing the vectors
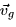 and
and  .
.