- (a)
- Find the equation of the plane that contains this line and the point (1,-1,1).
- (b)
- At what point(s) does this plane touch the coordinate axes?
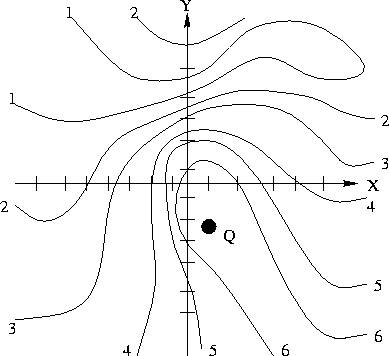
- (a)
- Does the surface corresponding to this diagram seem to be represented by a function? Why or why not?
- (b)
- Imagine pouring water onto the surface at point Q. Sketch the path of the water's flow, assuming that the water flows downhill along the steepest path.
- (c)
- Sketch a graph of the two sections x = 2 and y = 1.
![]()
![]()

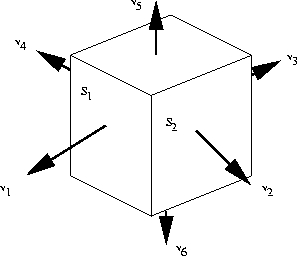
- (a)
- What is the vector
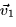 expressed as a unit vector?
expressed as a unit vector?
- (b)
- Give the vectors
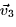 and
and 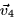 . Use
the fact that the faces of a cube are at right angles to each other.
. Use
the fact that the faces of a cube are at right angles to each other.
- (c)
- Using the fact that the faces of a cube meet at right angles, find
the vectors
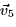 and
and 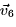 .
.