- (a)
- Find the equation of the plane parallel to this plane passing through the point (1, -1, 0).
- (b)
- What value(s) of t will make the plane -2x + ty - (t2 -3)z = 5 perpendicular to the first two planes?
- (a)
- Sketch cross sections of z = f(x,y) with x fixed.
- (b)
- Sketch cross sections of z = f(x,y) with y fixed.
- (c)
- Sketch a contour diagram of z = f(x,y) in the region
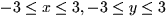 .
. - (d)
- If a drop of water is placed on the surface at x = y = 1 and always rolls down the steepest path, sketch the path of the water droplet with a dotted line on your contour diagram.
![]()
- (a)
- Find the equation of the surface in 3-space where the vector field has a constant magnitude of 1.
- (b)
- Describe the shape of the curves made where this surface touches the xy plane, the xz plane, and the yz plane.
![]()

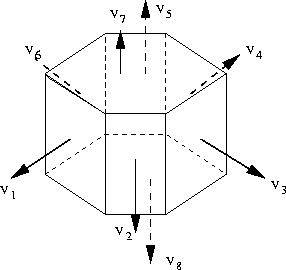
- (a)
- Express the vectors
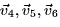 in terms of
the vectors
in terms of
the vectors 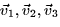 .
. - (b)
- Express
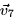 as a function of the vectors
as a function of the vectors 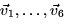 . You may not need all six of the other vectors to do this.
. You may not need all six of the other vectors to do this.
- (c)
- If
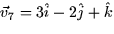 , what is
, what is
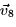 as a unit vector?
as a unit vector?